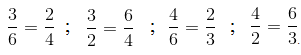a: \(\dfrac{15}{21}=\dfrac{5}{7}=\dfrac{30}{42}\)

=>Lập được TLT

b: \(\dfrac{0.25}{1.25}=\dfrac{1}{5}< >\dfrac{1}{7}\)

=>KO lập được TLT

c: \(0.4:\left(1+\dfrac{2}{5}\right)=0.4:1.4=\dfrac{2}{7}< >\dfrac{3}{5}\)

=>Ko lập được TLT

d: \(\dfrac{3}{5}:\dfrac{1}{7}=\dfrac{21}{5}=< >21:\dfrac{1}{5}\)

=>Ko lập được TLT

e: \(4+\dfrac{1}{2}:7+\dfrac{1}{2}=4.5:7.5=\dfrac{3}{5}< >\dfrac{2.7}{4.7}\)

=>Ko lập được TLT

f: 1/4:1/9=9/4

1/2:2/9=9/4

=>1/4:1/9=1/2:2/9

=>Lập được TLT

g: 2/7:4/11=2/7*11/4=22/28=11/14

7/2:4/11=7/2*11/4=77/8<>11/14

=>Ko lập được TLT

h: 2/5:10/2=2/5*2/10=4/50=2/25

2/1:1/4=8<>2/25

=>Ko lập được TLT

i: 2/7:7/4=2/7*4/7=8/49

16/49:2=8/49=2/7:7/4

=>Lập được TLT

Có!

Có lập được nha!

TẠI SAO

a) \(\dfrac{-2}{5}=\dfrac{-14}{35}\)

b) \(\dfrac{9}{4}=\dfrac{\dfrac{1}{4}}{\dfrac{1}{9}}\)

c) \(\dfrac{\dfrac{7}{4}}{\dfrac{1}{2}}=\dfrac{7}{2}\)

a)      Ta xét tỉ số \(\dfrac{6}{5}:2 = \dfrac{6}{5}.\dfrac{1}{2} = \dfrac{6}{{10}} = \dfrac{3}{5}\)

Tương tự xét với tỉ số \(\dfrac{{12}}{5}:4 = \dfrac{{12}}{5}.\dfrac{1}{4} = \dfrac{{12}}{{20}} = \dfrac{{12:4}}{{20:4}} = \dfrac{3}{5}\)

Ta thấy các tỉ số đều bằng \(\dfrac{3}{5}\) nên ta sẽ lập được một tỉ lệ thức : \(\dfrac{{12}}{5}:4\) = \(\dfrac{6}{5}:2\)

b)      Từ các số 9;2;3;6 ta thấy :

\(\dfrac{9}{3}\)= 3 và \(\dfrac{6}{2}\)=3 nên suy ra ta có tỉ lệ thức thứ nhất : \(\dfrac{9}{3}\)=\(\dfrac{6}{2}\)

Ta xét tỉ số \(\dfrac{9}{6}\)=\(\dfrac{{9:3}}{{6:3}}\)=\(\dfrac{3}{2}\)nên ta có được tỉ lệ thức thứ hai : \(\dfrac{9}{6}\)=\(\dfrac{3}{2}\)

3\6=2\4;2\3=4\6;4\6=2\3;4\2=6\3

\(\dfrac{3}{6}=\dfrac{2}{4};\dfrac{6}{3}=\dfrac{4}{2};\dfrac{3}{2}=\dfrac{6}{4};\dfrac{4}{6}=\dfrac{2}{3}\)

Gọi phân thức cần tìm là \(A\)

Ta có:

\(\dfrac{1}{x}.\dfrac{x}{x+1}.\dfrac{x+1}{x+2}.\dfrac{x+2}{x+3}.\dfrac{x+3}{x+4}.\dfrac{x+4}{x+5}.\dfrac{x+5}{x+6}.\dfrac{x+6}{x+7}.\dfrac{x+7}{x+8}.\dfrac{x+8}{x+9}.\dfrac{x+9}{x+10}\)

\(=\dfrac{x\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)\left(x+6\right)\left(x+7\right)\left(x+8\right)\left(x+9\right)}{\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)\left(x+6\right)\left(x+7\right)\left(x+8\right)\left(x+9\right)\left(x+10\right)}\)\(=\dfrac{x}{x+10}\)

Suy ra:

\(\dfrac{1}{x}.\dfrac{x}{x+1}.\dfrac{x+1}{x+2}.\dfrac{x+2}{x+3}.\dfrac{x+3}{x+4}.\dfrac{x+4}{x+5}.\dfrac{x+5}{x+6}.\dfrac{x+6}{x+7}.\dfrac{x+7}{x+8}.\dfrac{x+8}{x+9}.\dfrac{x+9}{x+10}.A=1\)

\(\Leftrightarrow\dfrac{x}{x+10}.A=1\)

\(\Leftrightarrow A=\dfrac{x+10}{x}\)

Vậy phân thức cần điền vào chỗ trống là \(\dfrac{x+10}{x}\)

\(P=\dfrac{1}{\sqrt{2}-\sqrt{3}}-\dfrac{1}{\sqrt{3}-\sqrt{4}}+\dfrac{1}{\sqrt{4}-\sqrt{5}}-...+\dfrac{1}{\sqrt{2n}-\sqrt{2n+1}}\)

\(P=\dfrac{\sqrt{2}+\sqrt{3}}{\left(\sqrt{2}+\sqrt{3}\right)\left(\sqrt{2}-\sqrt{3}\right)}-\dfrac{\sqrt{3}+\sqrt{4}}{\left(\sqrt{3}+\sqrt{4}\right)\left(\sqrt{3}-\sqrt{4}\right)}+...+\dfrac{\sqrt{2n}+\sqrt{2n+1}}{\left(\sqrt{2n}-\sqrt{2n+1}\right)\left(\sqrt{2n}+\sqrt{2n+1}\right)}\)

\(P=\dfrac{\sqrt{2}+\sqrt{3}}{2-3}-\dfrac{\sqrt{3}+\sqrt{4}}{3-4}+\dfrac{\sqrt{4}+\sqrt{5}}{4-5}-...+\dfrac{\sqrt{2n}+\sqrt{2n+1}}{2n-2n-1}\)

\(P=\dfrac{\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+\sqrt{4}+\sqrt{5}-...+\sqrt{2n}+\sqrt{2n+1}}{-1}\)

\(P=\dfrac{\sqrt{2}+\sqrt{2n+1}}{-1}\)

\(P=-\left(\sqrt{2}+\sqrt{2n+1}\right)\)

Mà: \(\sqrt{2}\) là số vô tỉ nên: \(-\left(\sqrt{2}+\sqrt{2n+1}\right)\) là số vô tỉ với mọi n

\(\Rightarrow\) P là số vô tỉ không phải là số hữu tỉ 

a) 2 phân số trên bằng nhau vì khi rút gọn \(\dfrac{6}{-27}\)với -3 ta được \(\dfrac{-2}{9}\)

=>\(\dfrac{-2}{9}=\dfrac{6}{-27}\)

b)-1/-5 và 4/25

-1/-5=-25/-125

4/25=-20/-125

=>-1/-5>4/25

\(a.\)

\(-\dfrac{2}{9}\)

\(\dfrac{-6}{27}=-\dfrac{2}{9}\)

\(\Rightarrow-\dfrac{2}{9}=-\dfrac{6}{27}\)

\(b.\)

\(\dfrac{-1}{-5}=\dfrac{1}{5}=\dfrac{5}{25}\)

\(\dfrac{4}{25}\)

\(\dfrac{5}{25}>\dfrac{4}{25}\)

\(\Rightarrow\dfrac{-1}{-5}>\dfrac{4}{25}\)