B1: Cho nửa đường tròn tâm o đường kính ab tiếp tuyến ax by . e thuộc ax , f thuộc by sao cho ae.bf=ab^2/4 chứng minh ef là tiếp tuyến
Help ! = t-i-c-k
. cho nửa đường tròn tâm O đường kính AB . lấy tia tiếp tuyên Ax , By với nửa đường tròn . lấy E thuộc nửa đường tron . Qua E vẽ tia tiếp tuyến với O cắt Ax tại D cắt By tại C
a) chứng minh OADE là tứ gics nội tiếp
b) AC cắt BD tại F , chứng minh EF//AD
1. Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax, By ( Ax, By cùng thuộc nửa mặt phẳng chứa nửa đường tròn bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại C và D.
a) Chứng minh đường tròn đường kính CD tiếp xúc với AB.
b) Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất.
c) Kẻ MH⊥AB tại H. Chứng minh rằng BC đi qua trung điểm I của MH.
(Chỉ cần làm câu c thôi mấy câu để có số liệu thôi)
c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm
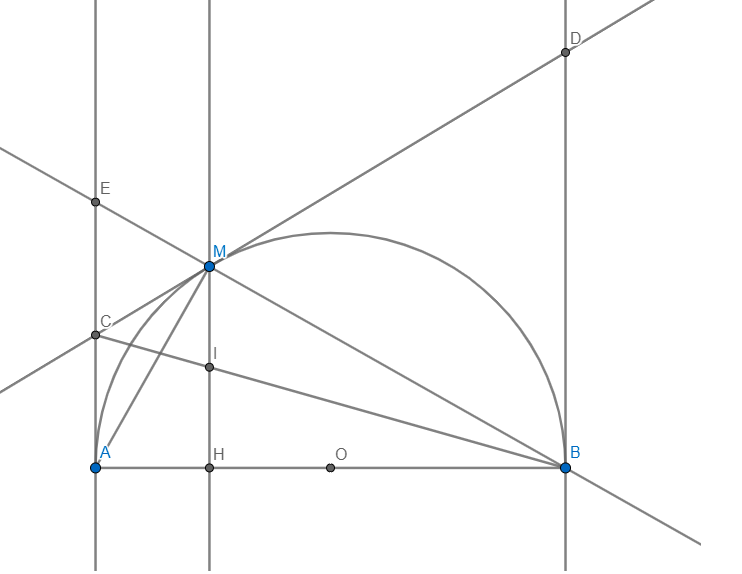
Cho đường tròn (O) đường kính AB. Vẽ Các tiếp tuyến Ax và By (Ax, By thuộc nửa mặt phẳng bờ AB). Qua điểm M trên (O) ( M khác A và B ) vẽ đường thẳng vuông góc với OM cắt Ax, By lần lượt tại E và F Chứng minh : a) EF là tiếp tuyến của đường tròn (O) b) EF = AE + BF
a: Xét (O) có
OM là bán kính
EF vuông góc OM tại M
Do đó: EF là tiếp tuyến của (O)
b: Xét (O) có
EM.EA là tiếp tuyến
nên EM=EA
Xét(O) có
FM,FB là tiếp tuyến
nên FM=FB
EF=EM+MF
=>EF=EA+FB
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB
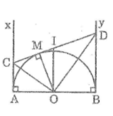
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
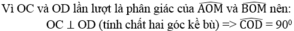
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.
Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax, By của nửa đường tròn. Kẻ tiếp tuyến tại M là 1 điểm bất kỳ thuộc đường tròn. Tiếp tuyến này cắt Ax, By thứ tự tại C, D. Chứng minh đường tròn đường kính CD tiếp xúc với AB
cho nửa đường tròn tâm O đường kính AB từ a,b kẻ 2 tiếp tuyến Ax và By qua điểm M thuộc nửa đường tròn tâm O kẻ tiếp tuyến thứ 3 cắt tiếp tuyến Ax và By lần lượt ở E và F
a) CM: AEMO nội tiếp
b) AM cắt OE ở P , BM cắt OF ở Q chứng minh MPOQ là HCN
a: góc EAO+góc EMO=180 độ
=>EAOM nội tiếp
b: góc AMB=1/2*sđ cung AB=90 độ
Xét (O) co
EM,EA là tiếptuyến
=>EM=EA
mà OM=OA
nên OE là trung trực của AM
=>OE vuông góc AM tại P
Xét (O) có
FM,FB là tiếptuyến
=>FM=FB
=>OF là trung trực của MB
=>OF vuông góc MB tại Q
góc MPO=góc MQO=góc PMQ=90 độ
=>MPOQ là hình chữ nhật
Cho nửa đường tròn tâm O đường kính AB. Vẻ các tiếp tuyến Ax, By của nửa đường tròn. Kẻ tiếp tuyến tại M thuộc nửa đường tròn. Tiếp tuyến này cắt Ax, By thứ tự tại C, D. Chứng minh rằng đường tròn đường kính CD tiếp xúc với AB.
Kẻ OI AB ( I CD) ta suy ra OI là đường trung bình của hình thang ABCD và CI = ID.
Khi đó I là tâm đường tròn đường kính CD và IO là khoảng cách d từ tâm I đến AB.
Ta có IO=CA+DB2 =MC+MD2 =DC2 là bán kính của đường tròn (I).
Do đó AB tiếp xúc với đường tròn đường kính CD.
Kẻ OI AB ( I CD) ta suy ra OI là đường trung bình của hình thang ABCD và CI = ID.
Khi đó I là tâm đường tròn đường kính CD và IO là khoảng cách d từ tâm I đến AB.
Ta có là bán kính của đường tròn (I).
Do đó AB tiếp xúc với đường tròn đường kính CD.
Gọi I là trung điểm của CD. (1)
Có O là trung điểm AB. (2)
Vì CA,CM,DM,DB là các tiếp tuyến đường tròn (O) thứ tự tại A,M,B
⇒ CA=CM, DB=DM; CA, DB cùng vuông góc với AB.
⇒ Tứ giác ACDB là hình thang vuông. (3)
Từ (1),(2),(3) ⇒ OI là đường trung bình của hình thang ACDB. (4)
⇒ OI = \(\dfrac{CA+DB}{2}\) = \(\dfrac{MC+MD}{2}\)
⇒ OI = DC : 2
⇒ OI là bán kính đường tròn đường kính DC. (5)
Từ (4) ⇒ OI vuông góc với AB tại O (6)
Từ (5) và (6) ⇒ AB tiếp xúc với đường tròn đường kính AB tại O.
Cho nửa đường tròn tâm O đường kính AB. Tia Ax và tia By song song, trên cung AB lấy điểm M bất kỳ tiếp tuyến tại M của đường tròn cắt Ax và By lần lượt tại E và F
Chứng minh AB là tiếp tuyến của đường tròn đường kính EF ( làm theo 2 cách)