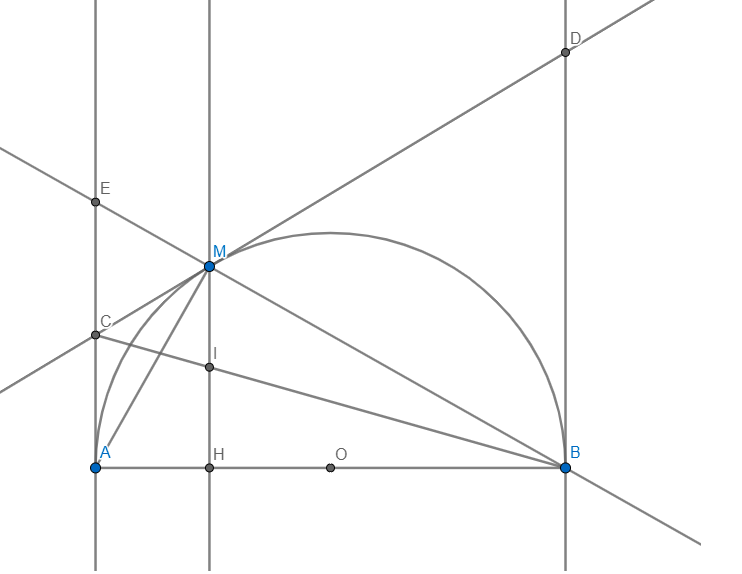
1. Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax, By ( Ax, By cùng thuộc nửa mặt phẳng chứa nửa đường tròn bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại C và D.
a) Chứng minh đường tròn đường kính CD tiếp xúc với AB.
b) Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất.
c) Kẻ MH⊥AB tại H. Chứng minh rằng BC đi qua trung điểm I của MH.
(Chỉ cần làm câu c thôi mấy câu để có số liệu thôi)
c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm