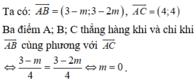trong một mặt phẳng Oxy cho A ( -2m; -m ), B ( 2m;m). Với giá trị nào của m thì đường thẳng AB đi qua O ?

Những câu hỏi liên quan
trong mặt phẳng tọa độ oxy cho 2 điểm A(m,2m+1) và B(m,2m2) chứng minh rằng điểm A luôn thuộc một đường thẳng cố định điểm B luôn thuộc một parabol cố định
giúp e với ạ
\(y_A-2x_A=2m+1-2m=1\)
\(\Rightarrow y_A=2x_A+1\) với mọi m hay A luôn thuộc đường thẳng cố định \(y=2x+1\)
\(\left\{{}\begin{matrix}x_B^2=m^2\\y_B=2m^2\end{matrix}\right.\) \(\Rightarrow y_B=2x_B^2\Rightarrow\) B luôn thuộc parabol cố định \(y=2x^2\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho A(m-1; -1) ; B(2; 2-2m) ; C(m+3; 3). Tìm giá trị m để A; B; C là ba điểm thẳng hàng?
A. m= 2
B. m=0
C. m=1
D. m=-2
Trong mặt phẳng oxy ,parabol (P) y=ax^2 (a khác 0 ) đi qua điểm M (-m;2m) với m >0 .Trong các điểm sau , điểm nào không thuộc đồ thị (P) ?
A,(-2m;8m).
B,(m;2m).
C,(2m;4m).
D,(0;0).
Trong mặt phẳng oxy ,parabol (P) y=ax^2 (a khác 0 ) đi qua điểm M (-m;2m) với m >0 .Trong cá điểm sau , điểm nào không thuộc đồ thị (P) ?
A,(-2m;8m).
B,(m;2m).
C,(2m;4m).
D,(0;0).
Trong không gian Oxy cho hai mặt phẳng (P); x-3y+2z+10 , (Q): (2m-1)x+m(1-2m)y+ (2m-4)z+140. Tìm m để (P) (Q) vuông góc với nhau A.
m
∈
1
;
-
3
2
B.
m
∈
1
;
3
2
C. ...
Đọc tiếp
Trong không gian Oxy cho hai mặt phẳng (P); x-3y+2z+1=0 , (Q): (2m-1)x+m(1-2m)y+ (2m-4)z+14=0. Tìm m để (P) (Q) vuông góc với nhau
A. m ∈ 1 ; - 3 2
B. m ∈ 1 ; 3 2
C. m ∈ - 1 ; - 3 2
D. m ∈ 2
Trong mặt phẳng toạ độ Oxy, cho (d) y=(m+5)x+2m-10. Tìm m để khoảng cách từ O đến d lớn nhất.
*TH1: m ≠ -5
Gọi M(xM; yM) là điểm cố định mà (d) đi qua với mọi m
=> xM; yM thoả mãn phương trình: yM = (m + 5)xM + 2m - 10 ∀m
⇔ yM = mxM + 5xM + 2m - 10 ∀m
⇔ m(xM + 2) + 5xM - yM - 10 = 0 ∀m
⇔ \(\left\{{}\begin{matrix}x_M+2=0\\5x_M-y_M-10=0\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x_M=-2\\y_M=-20\end{matrix}\right.\)
Vậy M(-2; -20) là điểm cố định mà (d) luôn đi qua với mọi m
=> OM = \(\sqrt{\left(x_O-x_M\right)^2+\left(y_O-y_M\right)^2}\) = \(\sqrt{2^2+20^2}\) = \(2\sqrt{101}\)
Gọi H là chân đường vuông góc hạ từ O xuống (d) => OH ≤ OM (tính chất đường vuông góc và đường xiên)
Vậy với m ≠ -5; khoảng cách lớn nhất từ O đến (d) là \(2\sqrt{101}\)
*TH2: m = -5
Với m = -5 ta có (d): y = 2.(-5) - 10 = -20
=> (d) // Ox và cắt Oy tại điểm có tung độ -20
=> Khoảng cách từ O đến (d) là 20
Ta có: 20 < \(2\sqrt{101}\) => Với m ≠ -5 thì khoảng cách từ O đến (d) là lớn nhất.
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ oxy cho (P):y = x^2 và (d): y = 2mx + 3 - 2m Chứng minh d luôn cắt P tại hai điểm mặt phẳng A và B. Tìm m để x1, x2 là độ dài hai cạnh của hình chữ nhật có đường chéo bằng √14
PTHĐGĐ là;
x^2-2mx-3+2m=0
Δ=(-2m)^2-4(2m-3)
=4m^2-8m+12
=4m^2-8m+4+8
=(2m-2)^2+8>0
=>(P) luôn cắt (d) tại hai điểm phân biệt
x1^2+x2^2=14
=>(x1+x2)^2-2x1x2=14
=>(2m)^2-2(2m-3)=14
=>4m^2-4m+6-14=0
=>4m^2-4m-8=0
=>m^2-m-2=0
=>(m-2)(m+1)=0
=>m=2 hoặc m=-1
Đúng 0
Bình luận (0)
GIÚP EM VỚI Ạ, CHIỀU NAY EM THI RỒI :(
Câu 3: Trong mặt phẳng Oxy, cho A( m - 1 ; -1 ) , B( 2; 2 - 2m ) , C( m + 3; 3 ). Tìm giá trị m để A, B, C là ba điểm thẳng hàng
A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
Đúng 1
Bình luận (0)
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy cho A(0;2), B(1;1); C(2m+1 ; m+7) biết điểm có tọa độ (2;4) là trọng tâm tam giác ABC, giá trị m = ...
Theo công thức trọng tâm:
\(\left\{{}\begin{matrix}\frac{0+1+2m+1}{3}=2\\\frac{2+1+m+7}{3}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2m+2=6\\m+10=12\end{matrix}\right.\) \(\Rightarrow m=2\)
Đúng 0
Bình luận (0)