Với giá trị nào của m thì phương trình (m-1) x2 -6(m-1) x+2m-3=0 có nghiệm kép

Những câu hỏi liên quan
Cho phương trình
(
m
+
2
)
x
2
+
(
2
m
+
1
)
x
+
2
0
Với giá trị nào của m thì phương trình có nghiệm kép? Tìm nghiệm kép đó
Đọc tiếp
Cho phương trình
( m + 2 ) x 2 + ( 2 m + 1 ) x + 2 = 0
Với giá trị nào của m thì phương trình có nghiệm kép? Tìm nghiệm kép đó
Phương trình có nghiệm kép khi m ≠ -2 và Δ = 0.
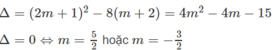
Khi m = 5/2 nghiệm kép của phương trình là
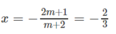
Khi m = -3/2 nghiệm kép của phương trình là x = 2.
Đúng 0
Bình luận (0)
Cho phương trình (ẩn x) x2 – 2(m – 1)x + m2 = 0
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 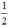
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 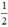
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 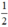
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 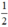 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 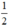 và vô nghiệm khi m >
và vô nghiệm khi m > 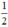
Đúng 0
Bình luận (0)
Với giá trị nào của m thì các phương trình sau có nghiệm kép m x 2 - 4(m - 1)x - 8 = 0
m x 2 – 4(m -1)x -8 =0 (2)
Phương trình (2) có nghiệm kép khi và chỉ khi: m ≠ 0 và ∆ '=0
Ta có: ∆ '= - 2 m - 1 2 – m(-8)=4( m 2 -2m +1) +8m
=4 m 2 – 8m +4 +8m = 4 m 2 +4
Vì 4 m 2 +4 luôn luôn lớn hơn 0 nên Δ' không thể bằng 0 .Vậy không có giá trị nào của m để phương trình có nghiệm kép
Đúng 0
Bình luận (0)
Với giá trị nào của m thì các phương trình sau có nghiệm kép 5 x 2 + 2mx – 2m +15 =0
5 x 2 + 2mx – 2m +15 =0 (1)
Ta có: ∆ '= m 2 – 5.(-2m +15) = m 2 +10m -75
Phương trình (1) có nghiệm kép khi và chỉ khi:
∆ '= 0 ⇔ m 2 + 10m – 75 = 0
∆ 'm = 5 2 -1.(-75) = 25 +75 = 100 > 0
∆ ' m = 100 =10
Phương trình có 2 nghiệm phân biệt:
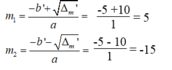
Vậy m =5 hoặc m=-15 thì phương trình đã cho có nghiệm kép
Đúng 0
Bình luận (0)
Cho phương trình (ẩn x) x 2 – 2 ( m – 1 ) x + m 2 = 0
a) Tính Δ'.
b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
a) Phương trình x 2 – 2 ( m – 1 ) x + m 2 = 0 (1)
Có a = 1; b’ = -(m – 1); c = m 2
b) Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 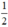
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 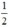
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 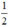
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 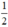 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 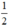 và vô nghiệm khi m >
và vô nghiệm khi m > 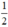
Đúng 0
Bình luận (0)
x^2-(2m+1)x+m^2=0(1)
a).Với giá trị của m thì phương trình (1) có nghiệm kép
\(\Delta=\left[-\left(2m+1\right)\right]^2-4m^2=4m^2+4m+1-4m^2=4m+1\)
Để (1) có nghiệm kép :
\(\Delta=0\Leftrightarrow4m+1=0\Leftrightarrow m=-\dfrac{1}{4}\)
Đúng 0
Bình luận (0)
1.Phương trình x^2 +5x -m -3 có nghiệm kép khi?
2.Cho pt x^2 - 5x+m-3 =0 (1)
1)Tìm m để pt có nghiệm kép. Tìm nghiệm kép đó.
2)Với giá trị nào của m thì phương trình (1) có 2 nghiệm phân biệt.
Giúp với ạ.
1.
xét delta có
25 -4(-m-3)
= 25 + 4m + 12
= 4m + 37
để phương trình có nghiệm kép thì delta = 0
=> 4m + 37 = 0 => m = \(\dfrac{-37}{4}\)
2.
a) xét delta
25 - 4(m-3) = 25 - 4m + 12 = -4m + 37
để phương trình có nghiệm kép thì delta = 0
=> -4m + 37 = 0
=> m = \(\dfrac{37}{4}\)
b)
xét delta
25 - 4(m-3) = 25 - 4m + 12 = -4m + 37
để phương trình có 2 nghiệm phân biệt thì delta > 0
=> -4m + 37 > 0
=> m < \(\dfrac{37}{4}\)
Đúng 0
Bình luận (0)
cho phương trình bậc hai x2-2(m-1)x+2m-5=0 (1)
với giá trị nào của m thì phương trình có hai nghiệm x1,x2 thỏa mãn:
x1<2<x2
Để phương trình (1) có nghiệm thì:
\(\Delta'\ge0\Rightarrow\left(m-1\right)^2-\left(2m-5\right)\ge0\)
\(\Leftrightarrow m^2-2m+1-2m+5\ge0\)
\(\Leftrightarrow\left(m-2\right)^2+2\ge0\) (luôn đúng)
Vậy với \(\forall m\) thì phương trình (1) luôn có nghiệm.
Theo định lí Vi-et cho phương trình (1) ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
Ta có: \(x_1< 2< x_2\Rightarrow\left\{{}\begin{matrix}x_1-2< 0\\x_2-2>0\end{matrix}\right.\)
\(\Rightarrow\left(x_1-2\right)\left(x_2-2\right)< 0\)
\(\Rightarrow x_1x_2-2\left(x_1+x_2\right)+4< 0\)
\(\Rightarrow2m-5-2.2\left(m-1\right)+4< 0\)
\(\Rightarrow2m-5-4m+4+4< 0\)
\(\Rightarrow-2m+3< 0\)
\(\Rightarrow m>\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Cho pt bậc hai ẩn x: x2 - 2mx + 2m - 1 = 0 (1)
a) Chứng minh pt (1) luôn có hai nghiệm x1, x2 với mọi giá trị của m.
b) Với giá trị nào của m thì pt (1) có hai nghiệm phân biệt ?
c) Trong trường hợp pt (1) có nghiệm kép. Hãy tính nghiệm kép đó.
d) Tìm m để pt (1) có nghiệm này bằng hai lần nghiệm kia (x1 = 2x2).
a, \(\Delta'=m^2-2m+1=\left(m-1\right)^2\)
Vậy pt luôn có 2 nghiệm
b, để pt có 2 nghiệm pb khi m khác 1
c, để pt có nghiệm kép khi m = 1
d. Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m\left(1\right)\\x_1x_2=2m-1\left(2\right)\end{matrix}\right.\)
Ta có \(x_1-2x_2=0\left(3\right)\)
Từ (1) ; (3) ta có \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1-2x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2=2m\\x_1=2m-x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2m-3\\x_1=2m-2m+3=3\end{matrix}\right.\)
Thay vào (2) ta được \(6m-9=2m-1\Leftrightarrow m=2\)
Đúng 1
Bình luận (0)
Cho phương trình 4x2-2(2m+3)x+m+1=0
a) với giá trị nào của m thì phương trình có một nghiệm bằng 0, tìm nghiệm còn lại
b) Trong trường hợp phương trình có 2 nghiệm x1 và x2, tìm tất cả các giá trị của m để (x1+x2) / (x1x2) < 4
MONG NHẬN ĐƯỢC SỰ GIÚP ĐỠ TỪ CÁC CAO NHÂN !!!
a) Thay x=0 vào phương trình, ta được:
\(4\cdot0^2-2\cdot\left(2m+3\right)\cdot0+m+1=0\)
\(\Leftrightarrow m+1=0\)
hay m=-1
Áp dụng hệ thức Vi-et, ta có:
\(x_1+x_2=\dfrac{2\left(2m+3\right)}{4}\)
\(\Leftrightarrow x_1=\dfrac{2\cdot\left(-2+3\right)}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
Vậy: Khi m=-1 và nghiệm còn lại là \(x=\dfrac{1}{2}\)
Đúng 0
Bình luận (1)
















