Câu d, bài 3 ạ

Những câu hỏi liên quan
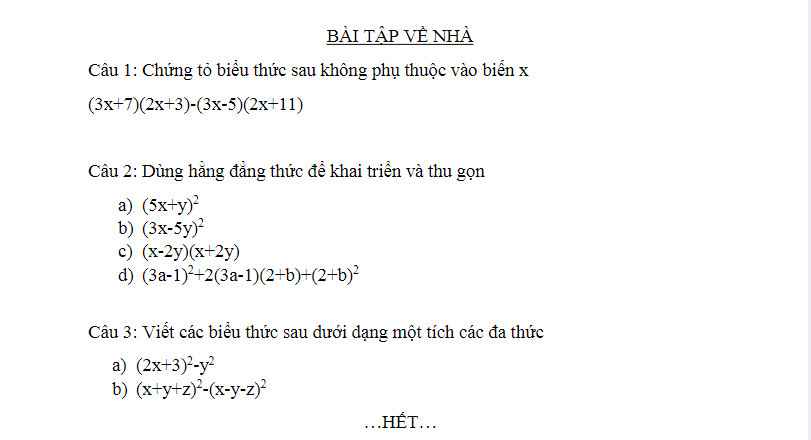
Câu 1:
Ta có: \(\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-\left(6x^2+33x-10x-55\right)\)
\(=6x^2+23x+21-6x^2-23x+55\)
=76
Đúng 1
Bình luận (2)
Mọi người giúp em câu c bài 3 với câu c,d bài 4 với ạ 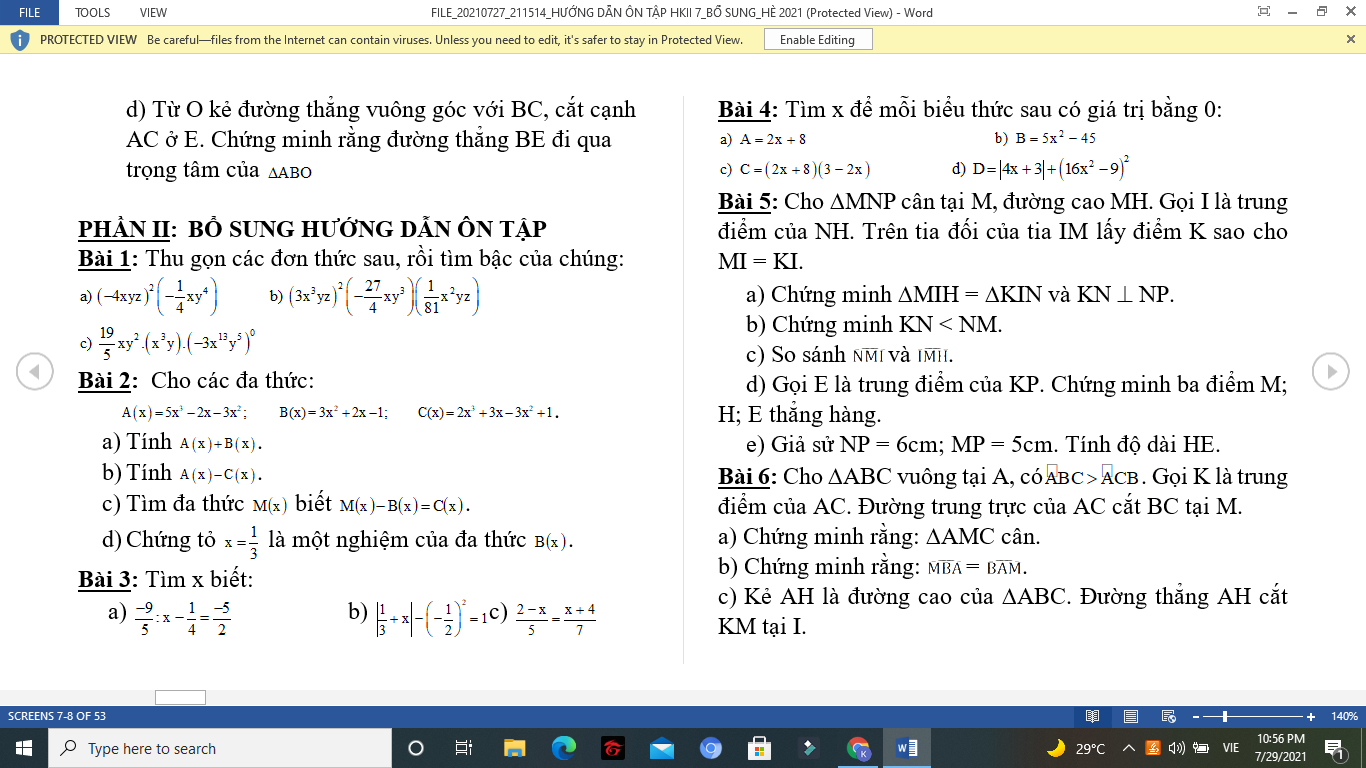
Bài 3:
c) Ta có: \(\dfrac{2-x}{5}=\dfrac{x+4}{7}\)
\(\Leftrightarrow14-7x=5x+20\)
\(\Leftrightarrow-7x-5x=20-14\)
\(\Leftrightarrow-12x=6\)
hay \(x=-\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Làm hộ mk câu D bài 3 vs ạ 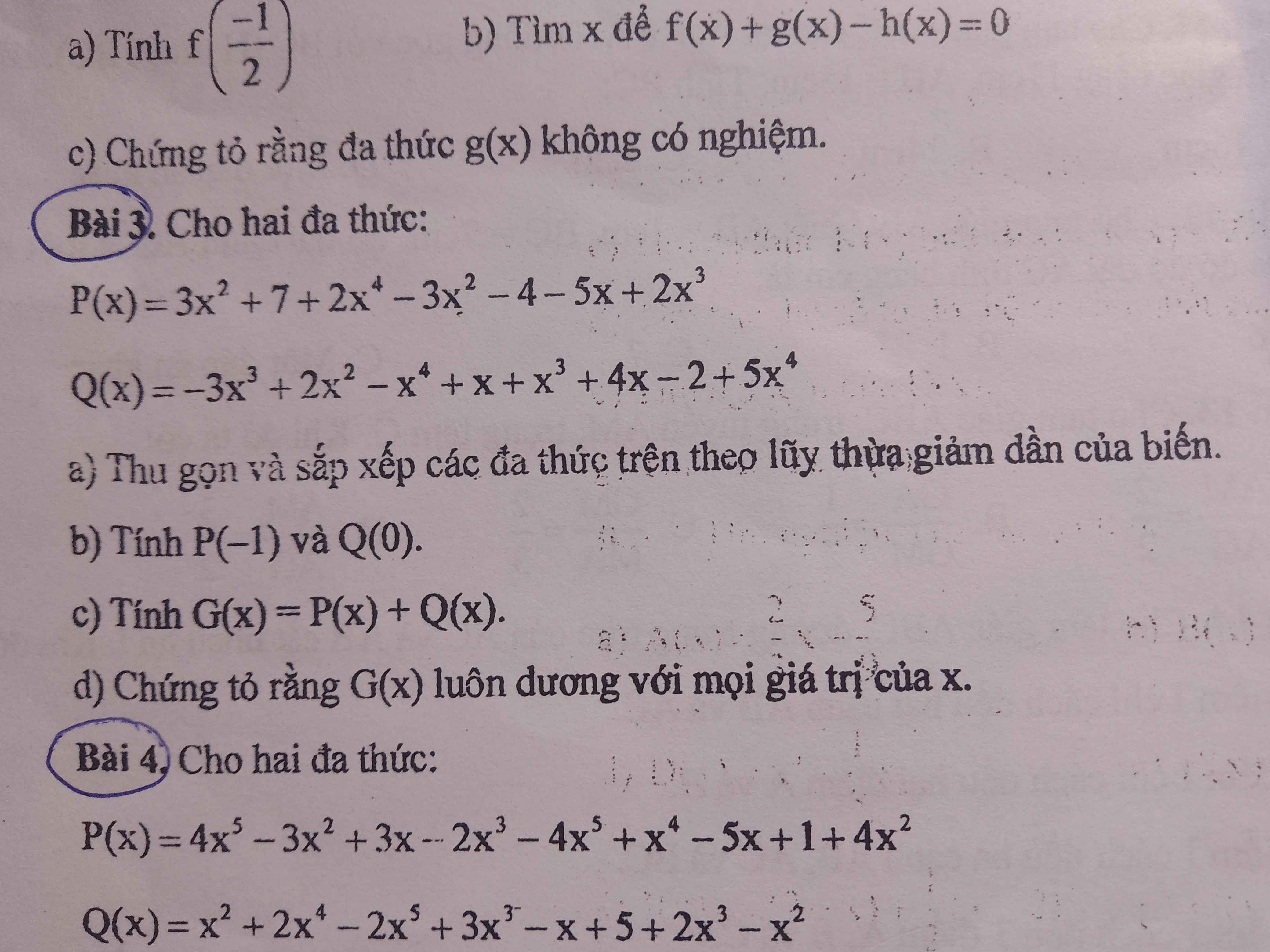
3:
a: \(P\left(x\right)=2x^4+2x^3-5x+3\)
\(Q\left(x\right)=4x^4-2x^3+2x^2+5x-2\)
b: P(-1)=2-2-3+5+3=5
Q(0)=4*0-2*0+2*0+5*0-2=-2
c: G(x)=2x^4+2x^3-5x+3+4x^4-2x^3+2x^2+5x-2
=6x^4+2x^2+1
d: G(x)=x^2(6x^2+2)+1>0 với mọi x
Đúng 0
Bình luận (0)
giúp em giải câu d bài 3 với ạ (nhớ tìm ĐKXĐ)

ĐIều kiện:`x^2-7x+8>=0`
`<=>x^2-2*x*7/2+49/4-17/4>=0`
`<=>(x-7/2)^2-17/4>=0`
`<=>(x-7/2)^2>=17/4`
`<=>|x-7/2|>=sqrt{17}/2`
`<=>` \(\left[ \begin{array}{l}x \ge \dfrac{7+\sqrt{17}}{2}\\x \le \dfrac{-\sqrt{17}+7}{2}\end{array} \right.\)
`pt<=>x^2-7x+sqrt{x^2-7x+8}-12=0`
`<=>x^2-7x+8+sqrt{x^2-7x+8}-20=0`
Đặt `a=sqrt{x^2-7x+8}(a>=0)`
`pt<=>a^2+a-20=0`
`<=>a=4(tm),a=-5(l)`
`<=>x^2-7x+8=16`
`<=>x^2-7x-8=0`
`a-b+c=0`
`=>x_1=-1(tm),x_2=8(tm)`
Vậy `S={-1,8}`
Đúng 2
Bình luận (0)
Bài 3 câu b và câu d
Bài 4 câu c và d
Bài 5 câu d,e,f giải
giúp mình với ạ cần gấp trong tối nay cả 3 bài

cái gì vậy bạn
? bài ở đâu
ko đăng ảnh đc ạ
Xem thêm câu trả lời
Làm giúp mik câu c, d (bài 3, màu trắng) và bài tập giải phương trình (màu trắng). Cảm ơn ạ

a. \(\sqrt{x^2-2x+4}=2x-2\)
<=> x2 - 2x + 4 = (2x - 2)2
<=> x2 - 2x + 4 = 4x2 - 8x + 4
<=> 4x2 - x2 - 8x + 2x + 4 - 4 = 0
<=> 3x2 - 6x = 0
<=> 3x(x - 2) = 0
<=> \(\left[{}\begin{matrix}3x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
b. \(\sqrt{x^2-2x}=\sqrt{2-3x}\)
<=> x2 - 2x = 2 - 3x
<=> x2 + 3x - 2x - 2 = 0
<=> x2 + x - 2 = 0
<=> x2 + 2x - x - 2 = 0
<=> x(x + 2) - (x + 2) = 0
<=> (x - 1)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
c. (Tương tự câu a)
Đúng 1
Bình luận (1)
e: Ta có: \(2\sqrt{9y-27}-\dfrac{1}{5}\sqrt{25y-75}-\dfrac{1}{7}\sqrt{49y-147}=0\)
\(\Leftrightarrow\sqrt{y-3}=0\)
hay y=3
Đúng 1
Bình luận (0)
Mọi ng giải mik câu(d) bài 11 và các câu của Bài 15 đc ko ạ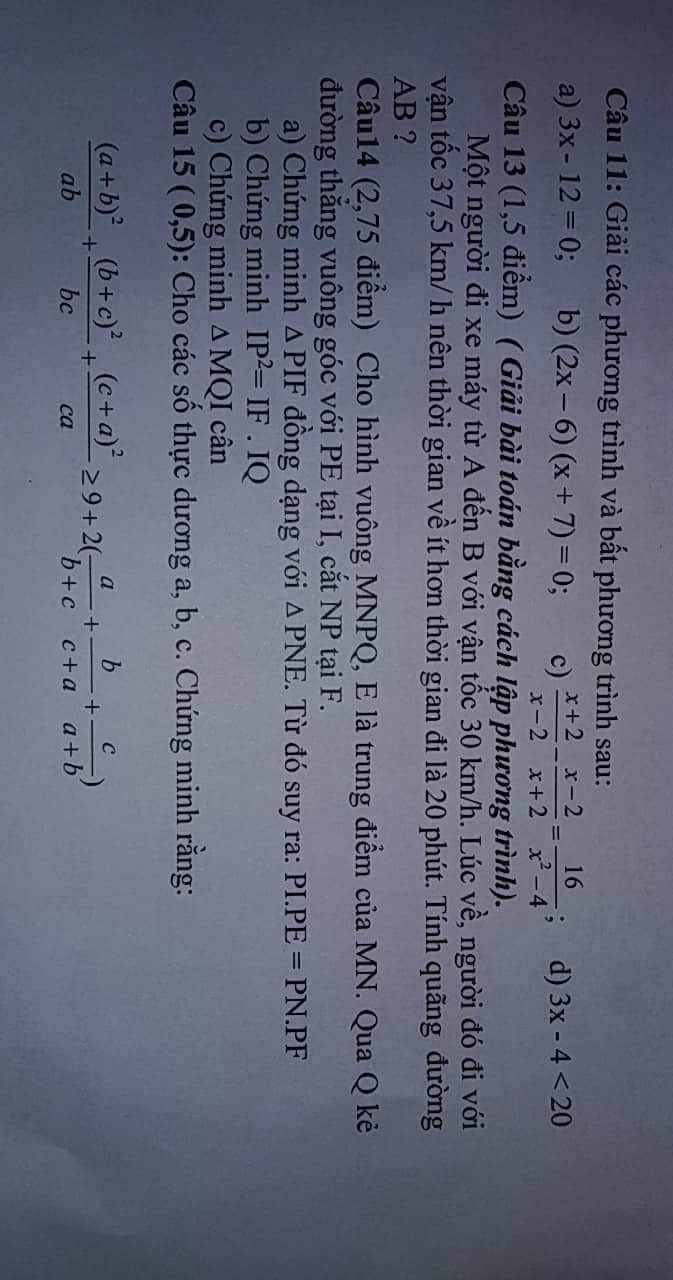
Câu 15: (mãi mới nghĩ ra :v)
\(\dfrac{\left(a+b\right)^2}{ab}+\dfrac{\left(b+c\right)^2}{bc}+\dfrac{\left(c+a\right)^2}{ca}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a^2+2ab+b^2}{ab}+\dfrac{b^2+2bc+b^2}{bc}+\dfrac{c^2+2ca+a^2}{ca}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a}{b}+2+\dfrac{b}{a}+\dfrac{b}{c}+2+\dfrac{c}{b}+\dfrac{c}{a}+2+\dfrac{a}{c}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{b}{c}+\dfrac{c}{b}+\dfrac{c}{a}+\dfrac{a}{c}\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{c}+\dfrac{1}{a}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
-Áp dụng BĐT Caushy Schwarz ta có:
\(\left\{{}\begin{matrix}\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1\right)^2}{b+c}=\dfrac{4}{b+c}\\\dfrac{1}{c}+\dfrac{1}{a}\ge\dfrac{\left(1+1\right)^2}{c+a}=\dfrac{4}{c+a}\\\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{\left(1+1\right)^2}{a+b}=\dfrac{4}{a+b}\end{matrix}\right.\)
-Từ đó suy ra: \(a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{c}+\dfrac{1}{a}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge\dfrac{4a}{b+c}+\dfrac{4b}{c+a}+\dfrac{4c}{a+b}\)
-Ta c/m rằng: \(\dfrac{4a}{b+c}+\dfrac{4b}{c+a}+\dfrac{4c}{a+b}\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\ge3\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+1+\dfrac{b}{c+a}+1+\dfrac{c}{a+b}+1-3\right)\ge3\)
\(\Leftrightarrow2\left(\dfrac{a+b+c}{b+c}+\dfrac{b+c+a}{c+a}+\dfrac{c+a+b}{a+b}\right)-6\ge3\)
\(\Leftrightarrow2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge9\left(1\right)\)
-Áp dụng BĐT Caushy Schwarz cho VT của BĐT ta được:
\(2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge2\left(a+b+c\right)\left(\dfrac{\left(1+1+1\right)^2}{a+b+b+c+c+a}\right)=2\left(a+b+c\right)\dfrac{9}{2\left(a+b+c\right)}=9\)
\(\Rightarrow\)BĐT (1) đúng.
\(\Rightarrowđpcm\)
-Dấu "=" xảy ra khi \(a=b=c\)
Đúng 0
Bình luận (0)
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
giúp em bài 1 câu c câu d với ạ!!!

`D=(sqrt{3}.sqrt{5-2sqrt6})/(sqrt3-sqrt2)-1/(2-sqrt3)`
`=(sqrt3*sqrt{3-2sqrt{3}.sqrt2+2})/(sqrt3-sqrt2)-(2+sqrt3)/(4-3)`
`=(sqrt3.sqrt{(sqrt3-sqrt2)^2})/(sqrt3-sqrt2)-2-sqrt3`
`=sqrt3-2-sqrt3=-2`
Đúng 1
Bình luận (3)
c) Ta có: \(C=\sqrt{\dfrac{3\sqrt{5}+1}{2\sqrt{5}-3}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{\left(3\sqrt{5}+1\right)\left(2\sqrt{5}-3\right)}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{30-9\sqrt{5}+2\sqrt{5}-3}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{27-7\sqrt{5}}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{54-14\sqrt{5}}}{2\sqrt{10}-3\sqrt{2}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\left(7-\sqrt{5}\right)\cdot\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{2}\cdot\left(2\sqrt{5}-3\right)}\)
\(=\dfrac{7\sqrt{5}-7-5+\sqrt{5}}{2\sqrt{5}-3}\)
\(=\dfrac{8\sqrt{5}-12}{2\sqrt{5}-3}\)
\(=\dfrac{4\left(2\sqrt{5}-3\right)}{2\sqrt{5}-3}=4\)
Đúng 0
Bình luận (0)
Mng hộ mik với ạ làm bài 5 bỏ câu c,d ạ
Đọc tiếp



Mng hộ mik với ạ làm bài 5 bỏ câu c,d ạ
a)2x2-7x-2x2-2x=7
-9x=7
x=-7/9
b)3x2+24x-x2-2x2-2x=2
22x=2
x=1/11
Đúng 1
Bình luận (0)
c: \(3x\left(x-7\right)-2\left(x-7\right)=0\)
\(\Leftrightarrow\left(x-7\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=\dfrac{2}{3}\end{matrix}\right.\)
d: \(7x^2-28=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)


























