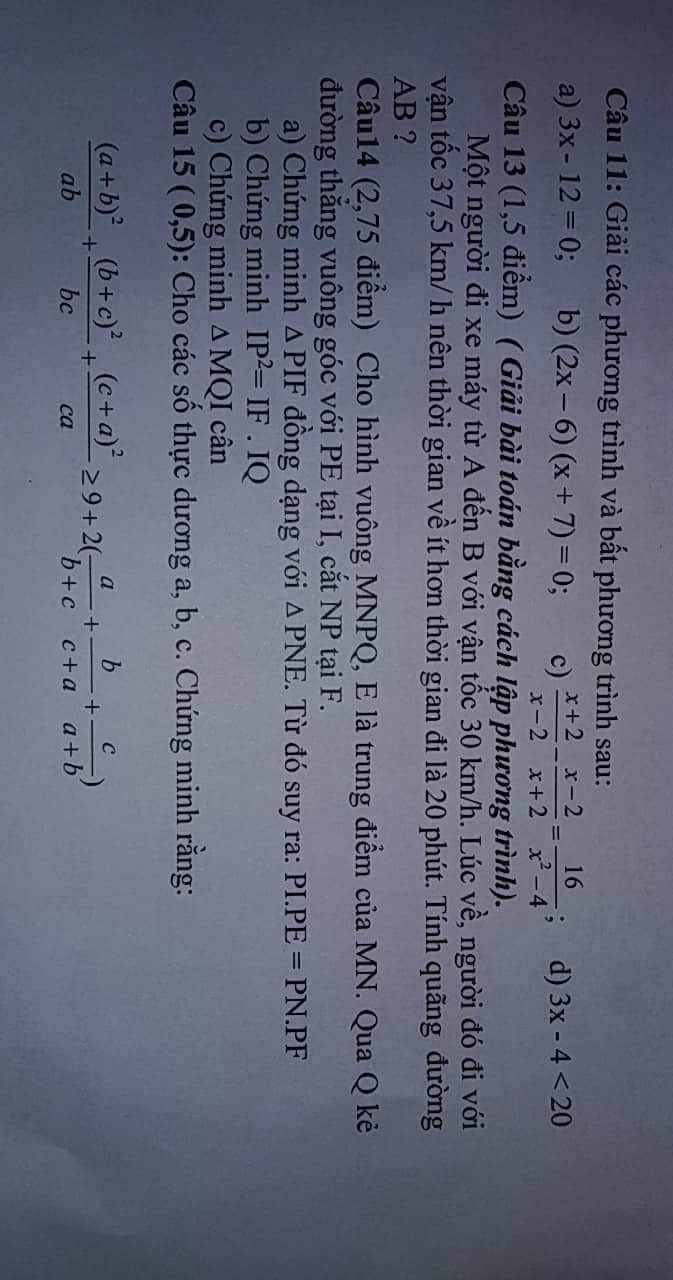Câu 15: (mãi mới nghĩ ra :v)
\(\dfrac{\left(a+b\right)^2}{ab}+\dfrac{\left(b+c\right)^2}{bc}+\dfrac{\left(c+a\right)^2}{ca}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a^2+2ab+b^2}{ab}+\dfrac{b^2+2bc+b^2}{bc}+\dfrac{c^2+2ca+a^2}{ca}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a}{b}+2+\dfrac{b}{a}+\dfrac{b}{c}+2+\dfrac{c}{b}+\dfrac{c}{a}+2+\dfrac{a}{c}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{b}{c}+\dfrac{c}{b}+\dfrac{c}{a}+\dfrac{a}{c}\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{c}+\dfrac{1}{a}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
-Áp dụng BĐT Caushy Schwarz ta có:
\(\left\{{}\begin{matrix}\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1\right)^2}{b+c}=\dfrac{4}{b+c}\\\dfrac{1}{c}+\dfrac{1}{a}\ge\dfrac{\left(1+1\right)^2}{c+a}=\dfrac{4}{c+a}\\\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{\left(1+1\right)^2}{a+b}=\dfrac{4}{a+b}\end{matrix}\right.\)
-Từ đó suy ra: \(a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{c}+\dfrac{1}{a}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge\dfrac{4a}{b+c}+\dfrac{4b}{c+a}+\dfrac{4c}{a+b}\)
-Ta c/m rằng: \(\dfrac{4a}{b+c}+\dfrac{4b}{c+a}+\dfrac{4c}{a+b}\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\ge3\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+1+\dfrac{b}{c+a}+1+\dfrac{c}{a+b}+1-3\right)\ge3\)
\(\Leftrightarrow2\left(\dfrac{a+b+c}{b+c}+\dfrac{b+c+a}{c+a}+\dfrac{c+a+b}{a+b}\right)-6\ge3\)
\(\Leftrightarrow2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge9\left(1\right)\)
-Áp dụng BĐT Caushy Schwarz cho VT của BĐT ta được:
\(2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge2\left(a+b+c\right)\left(\dfrac{\left(1+1+1\right)^2}{a+b+b+c+c+a}\right)=2\left(a+b+c\right)\dfrac{9}{2\left(a+b+c\right)}=9\)
\(\Rightarrow\)BĐT (1) đúng.
\(\Rightarrowđpcm\)
-Dấu "=" xảy ra khi \(a=b=c\)