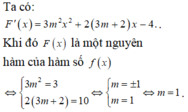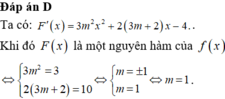Tìm GTNN của hàm số sau 3x2+\(\frac{4}{x}\)

Những câu hỏi liên quan
Tìm giá trị thực của m để hàm số
F
x
x
3
-
2
m
-
3
x
2
-
4
x
+
10
là một nguyên hàm của hàm số
f
x
3
x
2
-
12
x
-
4
với mọ...
Đọc tiếp
Tìm giá trị thực của m để hàm số F x = x 3 - 2 m - 3 x 2 - 4 x + 10 là một nguyên hàm của hàm số f x = 3 x 2 - 12 x - 4 với mọi x ∈ R
A. m = 3 2
B. m = - 9 2
C. m = 9 2
D. m = 9
tính đạo hàm của hàm số sau: (3x2+4).\(\sqrt{x}\)
\(y'=\left(3x^2+4\right)'\sqrt{x}+\left(3x^2+4\right).\left(\sqrt{x}\right)'=6x\sqrt{x}+\dfrac{3x^2+4}{2\sqrt{x}}=\dfrac{15x^2+4}{2\sqrt{x}}\)
Đúng 0
Bình luận (0)
Tìm GTNN của hàm số \(3x^2+\frac{4}{x}\)
Ta có \(3-\frac{8}{x^3}\)
\(=0=3-\frac{8}{x^3}=0=x=\frac{2}{^3\sqrt{3}}=y=\frac{9}{^3\sqrt{3}}=3^3\sqrt{9}\)
Vậy \(min\)của hàm số \(3x^2+\frac{4}{x}=3^3\sqrt{9}\)
Tìm giá trị của m để hàm số
F
(
x
)
m
2
x
3
+
(
3
m
+
2
)
x
2
-
4
x
+
3
là một nguyên hàm của hàm số
f
(
x
)
3
x
2...
Đọc tiếp
Tìm giá trị của m để hàm số F ( x ) = m 2 x 3 + ( 3 m + 2 ) x 2 - 4 x + 3 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 10 x - 4
A. m = 2
B. m = ± 1
C. m = -1
D. m = 1
Tìm giá trị của m để hàm số F(x)
m
2
x
3
+
(
3
m
+
2
)
x
2
-
4
x
+
3
là một nguyên hàm của hàm số f(x)
3
x
2
+
10
x
-
4
. A. m 2. B.
m
±
1
....
Đọc tiếp
Tìm giá trị của m để hàm số F(x) = m 2 x 3 + ( 3 m + 2 ) x 2 - 4 x + 3 là một nguyên hàm của hàm số f(x) = 3 x 2 + 10 x - 4 .
A. m = 2.
B. m = ± 1 .
C. m = -1.
D. m = 1.
Tìm số thực m để hàm số
F
(
x
)
m
x
3
+
(
3
m
+
2
)
x
2
-
4
x
+
3
là một nguyên hàm của hàm số
f
(
x
)
3
x
2
+
10
x
-...
Đọc tiếp
Tìm số thực m để hàm số F ( x ) = m x 3 + ( 3 m + 2 ) x 2 - 4 x + 3 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 10 x - 4 ?
A. m = -1.
B. m = 0.
C. m = 1.
D. m = 2.
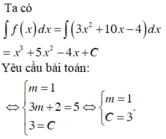
Vậy m =1 là giá trị cần tìm thỏa mãn yêu cầu bài toán.
Đáp án C
Đúng 0
Bình luận (0)
Tìm giá trị thực của m để hàm số F(x) x3 – (2m – 3)2 – 4x + 10 là một nguyên hàm của hàm số f(x) 3x2 – 12x – 4 với mọi
x
∈
ℝ
A.
m
3
2
B.
m
-
9
2
C.
m
9
2
D.
m...
Đọc tiếp
Tìm giá trị thực của m để hàm số F(x) = x3 – (2m – 3)2 – 4x + 10 là một nguyên hàm của hàm số f(x) = 3x2 – 12x – 4 với mọi x ∈ ℝ
A. m = 3 2
B. m = - 9 2
C. m = 9 2
D. m = 9
xét tính chẵn lẻ của hàm số sau :
\(y=\frac{3tan^3x-5sinx}{2+cosx}\)
\(y=\frac{sinx}{x^4-3x^2+2}\)
Tìm GTLN GTNN của hàm số sau
y= sinx + cosx
\(y=\sqrt{2cosx+3}-4\)
\(y=sin^4x+cos^4x\)
Xét tính chẵn lẻ:
a) TXĐ: D = R \ {π/2 + kπ| k nguyên}
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{3\tan^3\left(-x\right)-5\sin\left(-x\right)}{2+\cos\left(-x\right)}=-\frac{3\tan^3x-5\sin x}{2+\cos x}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
b) TXĐ: D = R \ \(\left\{\pm\sqrt{2};\pm1\right\}\)
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{\sin\left(-x\right)}{\left(-x\right)^4-3\left(-x\right)^2+2}=-\frac{\sin x}{x^4-3x^2+2}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
Đúng 0
Bình luận (0)
Tìm GTLN, GTNN:
TXĐ: D = R
a) Ta có (\(\left(\sin x+\cos x\right)^2=1+\sin2x\)
Với mọi x thuộc D ta có\(-1\le\sin2x\le1\Leftrightarrow0\le1+\sin2x\le2\Leftrightarrow0\le\left(\sin x+\cos x\right)^2\le2\)
\(\Leftrightarrow0\le\left|\sin x+\cos x\right|\le\sqrt{2}\Leftrightarrow-\sqrt{2}\le\sin x+\cos x\le\sqrt{2}\)
Vậy \(Min_{f\left(x\right)}=-\sqrt{2}\) khi \(\sin2x=-1\Leftrightarrow2x=-\frac{\pi}{2}+k2\pi\Leftrightarrow x=-\frac{\pi}{4}+k\pi\)
\(Max_{f\left(x\right)}=\sqrt{2}\) khi\(\sin2x=1\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
b) Với mọi x thuộc D ta có:
\(-1\le\cos x\le1\Leftrightarrow-2\le2\cos x\le2\Leftrightarrow1\le2\cos x+3\le5\)
\(\Leftrightarrow1\le\sqrt{2\cos x+3}\le\sqrt{5}\Leftrightarrow5\le\sqrt{2\cos x+3}+4\le\sqrt{5}+4\)
Vậy\(Min_{f\left(x\right)}=5\) khi \(\cos x=-1\Leftrightarrow x=\pi+k2\pi\)
\(Max_{f\left(x\right)}=\sqrt{5}+4\) khi \(\cos x=1\Leftrightarrow x=k2\pi\)
c) \(y=\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x\cos^2x\)\(=1-\frac{1}{2}\left(2\sin x\cos x\right)^2=1-\frac{1}{2}\sin^22x\)
Với mọi x thuộc D ta có: \(0\le\sin^22x\le1\Leftrightarrow-\frac{1}{2}\le-\frac{1}{2}\sin^22x\le0\Leftrightarrow\frac{1}{2}\le1-\frac{1}{2}\sin^22x\le1\)
Đến đây bạn tự xét dấu '=' xảy ra khi nào nha :p
Đúng 0
Bình luận (0)
Tìm khẳng định đúng trong các khẳng định sau đây:A. Hàm số y
x
3
- 5 có hai cực trị;B. Hàm số y
x
4
/4 + 3
x
2
- 5 luôn đồng biến;C. Tiệm cận ngang của đồ thị hàm số
y
3
x
-...
Đọc tiếp
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số y = 3 x - 2 5 - x là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
y
=
3
x
2
-
2
x
+
5
x
2
+
x
+
7
Đáp án: C.
y = -3 là tiệm cận ngang của đồ thị hàm số
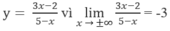
Đúng 0
Bình luận (0)
Tìm nguyên hàm của hàm số sau:
∫
x
4
-
3
x
2
+
2
x
+
1
d
x
A.
x
5
5
-
x
3...
Đọc tiếp
Tìm nguyên hàm của hàm số sau: ∫ x 4 - 3 x 2 + 2 x + 1 d x
A. x 5 5 - x 3 + x 2 + 2 x + C
B. x 5 5 + x 3 + x 2 + x + C
C. x 5 5 - x 3 + x 2 - x + C
D. x 5 5 - x 3 + x 2 + x + C
Chọn D
∫ x 4 - 3 x 2 + 2 x + 1 d x = ∫ x 4 d x - 3 ∫ x 2 d x + 2 ∫ x d x + ∫ d x = x 5 5 - x 3 + x 2 + x + C
Đúng 0
Bình luận (0)