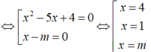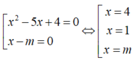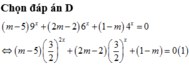Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2-2|x|+1-m =0 có 4 nghiệm phân biệt

Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
Đặt \(\left|x\right|=t\ge0\)
\(\Rightarrow t^2-2t+1-m=0\) (1)
Phương trình (1) là bậc 2 nên có đối đa 2 nghiệm t
Với mỗi giá trị \(t>0\) cho 2 nghiệm x tương ứng nên pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(1-m\right)>0\\t_1+t_2=2>0\\t_1t_2=1-m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< 1\end{matrix}\right.\) \(\Leftrightarrow0< m< 1\)
Đúng 1
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
1.Cho phương trình x2 +4x-m=0(1).Tìm tất cả các giá trị của tham số m để phương trinh (1) có đúng 1 nghiệm thuộc khoảng (-3,1)
2.Có bao nhiêu giá trị m nguyên trong nửa khoảng (0;2019] để phương trình |x2 -4|x|-5|-m có hai nghiệm phân biệt
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình
(
x
2
-
5
x
+
4
)
x
-
m
0
có đúng hai nghiệm phân biệt. A. 4 B. 2 C. 3 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình ( x 2 - 5 x + 4 ) x - m = 0 có đúng hai nghiệm phân biệt.
A. 4
B. 2
C. 3
D. 1
bao nhiêu giá trị nguyên của tham số m để phương trình
(
x
2
-
5
x
+
4
)
x
-
m
0
có đúng hai nghiệm phân biệt. A. 4 B. 2 C. 3 D. 1
Đọc tiếp
bao nhiêu giá trị nguyên của tham số m để phương trình ( x 2 - 5 x + 4 ) x - m = 0 có đúng hai nghiệm phân biệt.
A. 4
B. 2
C. 3
D. 1
Cho phương trình \(x^2-2x-2\left|x-m\right|+1=0\) Có bao nhiêu giá trị của tham số m để có 3 nghiệm thực phân biệt
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)
Cho phương trình: (3. 2x. lg x - 12lg x - 2x + 4)\(\sqrt{5^x-m}\) = 0 (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để pt đã cho có đúng 2 nghiệm phân biệt?
\(\Leftrightarrow\left\{{}\begin{matrix}3.2^xlogx-12logx-2^x+4=0\left(1\right)\\5^x=m\left(2\right)\end{matrix}\right.\) và \(5^x\ge m\) (\(x>0\))
Xét (1):
\(\Leftrightarrow3logx\left(2^x-4\right)-\left(2^x-4\right)=0\)
\(\Leftrightarrow\left(3logx-1\right)\left(2^x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=\sqrt[3]{10}\end{matrix}\right.\)
\(y=5^x\) đồng biến trên R nên (2) có tối đa 1 nghiệm
Để pt đã cho có đúng 2 nghiệm phân biệt ta có các TH sau:
TH1: (2) vô nghiệm \(\Rightarrow m\le0\) (ko có số nguyên dương nào)
TH2: (2) có nghiệm (khác với 2 nghiệm của (1)), đồng thời giá trị của m khiến cho đúng 1 nghiệm của (1) nằm ngoài miền xác định
(2) có nghiệm \(\Rightarrow m>0\Rightarrow x_3=log_5m\)
Do \(\sqrt[3]{10}>2\) nên bài toán thỏa mãn khi: \(x_1< x_3< x_2\)
\(\Rightarrow2< log_5m< \sqrt[3]{10}\)
\(\Rightarrow25< m< 5^{\sqrt[3]{10}}\) (hơn 32 chút xíu)
\(\Rightarrow\) \(32-26+1\) giá trị nguyên
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên trong đoạn
-
2018
;
2018
của tham số m để phương trình
3
x
2
-
3
m
x
+
1
3
3
x
3
+
x
có 2 nghiệm phân biệt? A. 4036 B. 4037 C. 2019 D. 2020
Đọc tiếp
Có bao nhiêu giá trị nguyên trong đoạn - 2018 ; 2018 của tham số m để phương trình 3 x 2 - 3 m x + 1 = 3 3 x 3 + x có 2 nghiệm phân biệt?
A. 4036
B. 4037
C. 2019
D. 2020
Chọn đáp án C.

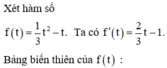
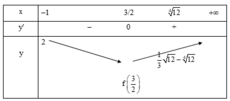

Bình luận:



Quay lại với lời giải ở trên: Ta chia cả 2 vế của (*) cho x chính là chia cả 2 vế của (2) cho
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình
(
m
-
5
)
9
x
+
(
2
m
-
2
)
6
x
+
(
1
-
m
)
4
x
0
có hai nghiệm phân biệt? A. 2 B. 4 C. 3 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình ( m - 5 ) 9 x + ( 2 m - 2 ) 6 x + ( 1 - m ) 4 x = 0 có hai nghiệm phân biệt?
A. 2
B. 4
C. 3
D. 1