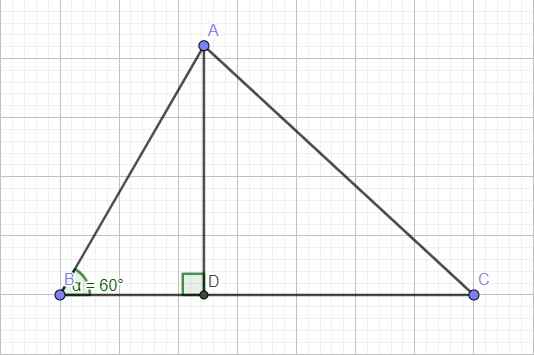
cho ΔABC có góc B =60o , AB=6cm,AC=4cm . tính AC (ΔABC không vuông)

Những câu hỏi liên quan
Cho ΔABC có góc B =\(60^o\) , BC=6cm, AC=4cm . Tính AC (ΔABC không vuông)
Kẻ đường cao AH
Ta thấy :
\(\frac{BH}{AB}=cosB\Rightarrow BH=ABcosB=6cos60^o=3\left(cm\right)\)
\(\frac{AH}{AB}=sinB\Rightarrow AH=ABsinB=6sin60^o=3\sqrt{3}\left(cm\right)\)
\(CH=BC-BH=4-3=1\left(cm\right)\)
Áp dụng định lí Pitago cho tam giác vuông AHC
\(AC=\sqrt{AH^2+CH^2}=\sqrt{\left(3\sqrt{3}^2\right)+1^2}=2\sqrt{7}\left(cm\right)\)
Chúc bạn học tốt !!!
cho ΔABC có góc B bằng 60o, BC=8cm, AB+AC=12cm. Tính AB,AC
Kẻ đường cao AD, đặt \(AB=x>0\) ; \(BD=y>0\)
\(\Rightarrow AC=12-x\) ; \(CD=8-y\)
Trong tam giác vuông ABD:
\(BD=AB.cosB\Leftrightarrow y=x.cos60^0=\dfrac{x}{2}\) \(\Rightarrow CD=8-\dfrac{x}{2}\)
Theo định lý Pitago:
\(\left\{{}\begin{matrix}AD^2=AB^2-BD^2\\AD^2=AC^2-CD^2\end{matrix}\right.\) \(\Rightarrow AB^2-BD^2=AC^2-CD^2\)
\(\Leftrightarrow x^2-\left(\dfrac{x}{2}\right)^2=\left(12-x\right)^2-\left(8-\dfrac{x}{2}\right)^2\)
\(\Leftrightarrow16x-80=0\)
\(\Rightarrow x=5\)
Vậy \(\left\{{}\begin{matrix}AB=5\\AC=7\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho ΔABC có góc A = \(50^o\), AB = 4cm, AC = 6cm. Tính diện tích tam giác ABC.
Để tính diện tích tam giác ABC, chúng ta có thể sử dụng công thức diện tích tam giác:
Diện tích tam giác ABC = 1/2 * AB * AC * sin(A)
Với góc A = 50°50' và AB = 4cm, AC = 6cm, chúng ta có thể tính được diện tích tam giác ABC bằng cách thay các giá trị vào công thức trên.
Đúng 0
Bình luận (0)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=\dfrac{1}{2}\cdot4\cdot6\cdot sin50\simeq9,19\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A có AB=AC=6cm, BC=4cm. Tính bán kính đường tròn tìm ngoại tiếp ΔABC
Gọi O là tâm đường tròn ngoại tiếp ΔABC
Gọi H là giao của AO với BC
AB=AC
OB=OC
Do đó: AO là trung trực của BC
=>AH là trung trực của BC
=>H là trung điểm của BC
HB=HC=4/2=2cm
Kẻ giao của AO với (O) là D
=>AD là đường kính của (O)
Xét (O) có
ΔABD nội tiếp
ADlà đường kính
Do đó: ΔBAD vuông tại B
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>\(AH^2=6^2-2^2=32\)
=>\(AH=4\sqrt{2}\left(cm\right)\)
Xét ΔBAD vuông tại B có BH là đường cao
nên AB^2=AH*AD
=>\(AD=\dfrac{6^2}{4\sqrt{2}}=\dfrac{9}{\sqrt{2}}\left(cm\right)\)
=>\(R=\dfrac{AD}{2}=\dfrac{9}{2\sqrt{2}}\left(cm\right)\)
Đúng 0
Bình luận (0)
1.
a) Cho ΔABC có : AC=5cm, BC=3cm. Tìm cạnh AB biết, AB là số nguyên và AB>6cm
b) Cho ΔABC có: AB=8cm, AC=6cm. Tính BC, biết BC là số nguyên BC<4cm
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A có AB > AC, M là điểm tuỳ ý trên BC. Qua M kẻ Mx vuông góc với BC và cắt AB tại I cắt CA tại D.
a. Chứng minh ΔABC đồng dạng với ΔMDC
b. Chứng minh: BI.BA = BM.BC
c. Cho góc ACB = 60o và SΔCDB = 60 cm². Tính SΔCMA.
a: Xét ΔCMD vuông tại M và ΔCAB vuông tại A có
góc C chung
=>ΔCMD đồng dạng với ΔCAB
b: Xét ΔBMI vuông tại M và ΔBAC vuông tại A có
góc MBI chung
=>ΔBMI đồng dạng với ΔBAC
=>BM/BA=BI/BC
=>BM*BC=BA*BI
c: ΔCMD đồng dạng với ΔCAB
=>CM/CA=CD/CB
=>CM/CD=CA/CB
=>ΔCMA đồng dạng với ΔCDB
=>S CMA/S CDB=(CA/CB)^2=1/4
=>S CMA=15cm2
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A, có AH vuông góc BC. Tính AB biết HB = 2cm; HC=8cm, AC=6cm
\(BC=BH+HC=2+8=10\left(cm\right)\)
△ABC vuông tại A có \(BC^2=AB^2+AC^2\\ \Rightarrow AB^2=BC^2-AC^2=10^2-6^2=64\\ \Rightarrow AB=8\left(cm\right)\)
Đúng 2
Bình luận (0)
vẽ ΔABC vuông góc tại A có AB= 3cm; AC= 4cm. Tính BC
Vì \(\Delta ABC\) vuông tại \(A\)
\(\Rightarrow\) \(AB , AC\) là hai cạnh góc vuông còn \(BC\) là cạnh huyền
Áp dụng định lý Py \(-\) ta \(-\) go vào \(\Delta ABC\) , ta có :
\(BC^2=AB^2+AC^2=3^2+4^2=9+16=25=5^2\)
\(\Rightarrow\) \(BC=5\)
Vậy \(BC = 5 cm\)
Đúng 0
Bình luận (0)
Cho ΔABC có 3 góc nhọn (AB < AC). Gọi BD là đường phân giác trong của ΔABC, dựng đường trung trực của đường thẳng BD cắt đường thẳng AC tại M.
a) Cm: ΔMAB đồng dạng ΔMBC.
b) Cho AD = 4cm, DC = 6cm. Tính MD.
Cho ΔABC có AB = 4cm , AC = 5cm , BC = 6cm .Trên tia đối của tia AB lấy D sao cho AD=5cm
a)Chứng minh :△ABC∞ΔCBD
b) Tính CD
c)Chứng minh góc BAC = 2. góc ACD
a, \(\Delta ABC\sim\Delta CBD\)
\(\dfrac{AB}{CB}=\dfrac{BC}{BD}=\dfrac{4}{6}=\dfrac{6}{4+5}=\dfrac{2}{3}\)
b, \(\dfrac{AC}{CD}=\dfrac{AB}{CB}=\dfrac{2}{3}\)
\(\Rightarrow CD=\dfrac{3AC}{2}=\dfrac{15}{2}\)
-Chúc bạn học tốt-
Đúng 1
Bình luận (0)