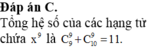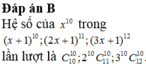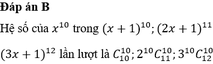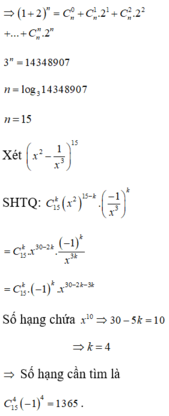tìm hệ số của x10 trong khai triển (1+x+x2)10

Những câu hỏi liên quan
a)Tìm số hạng không chứa x trong khai triển (x+2/x)10
b)Tìm số hạng không chứa x trong khai triển (x+2/x2)6
c)Tìm hệ số của số hạng chứa x10 trong khai triển (3x3-2/x2)5
a: SHTQ là: \(C^k_{10}\cdot x^{10-k}\cdot\left(\dfrac{2}{x}\right)^k=C^k_{10}\cdot2^k\cdot x^{10-2k}\)
Số hạng ko chứa x tương ứng với 10-2k=0
=>k=5
=>SH đó là 8064
b: SHTQ là; \(C^k_6\cdot x^{6-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_6\cdot2^k\cdot x^{6-3k}\)
Số hạng ko chứa x tương ứng với 6-3k=0
=>k=2
=>Số hạng đó là 60
c: SHTQ là: \(C^k_5\cdot\left(3x^3\right)^{5-k}\cdot\left(-\dfrac{2}{x^2}\right)^k\)
\(=C^k_5\cdot3^{5-k}\cdot\left(-2\right)^k\cdot x^{15-5k}\)
SH chứa x^10 tương ứng với 15-5k=10
=>k=1
=>Hệ số là -810
Đúng 1
Bình luận (0)
Tìm hệ số chứa
x
9
trong khai triển của
P
(
x
)
1
+
x
9
+
1
+
x
10
A. 10 B. 12 C. 11 D. 13
Đọc tiếp
Tìm hệ số chứa x 9 trong khai triển của P ( x ) = 1 + x 9 + 1 + x 10
A. 10
B. 12
C. 11
D. 13
Hệ số của số hạng chứa
x
10
trong khai triển
(
x
+
1
)
10
+
(
2
x
+
1
)
11
+
(
3
x
+
1...
Đọc tiếp
Hệ số của số hạng chứa x 10 trong khai triển ( x + 1 ) 10 + ( 2 x + 1 ) 11 + ( 3 x + 1 ) 12 là
![]()
![]()
![]()
![]()
Hệ số của số hạng chứa
x
10
trong khai triển
(
x
+
1
)
10
+
(
2
x
+
1
)
11
+
(
3
x
+
1
)
12
là A.
C
10
10
+
C
11...
Đọc tiếp
Hệ số của số hạng chứa x 10 trong khai triển ( x + 1 ) 10 + ( 2 x + 1 ) 11 + ( 3 x + 1 ) 12 là
A. C 10 10 + C 11 10 + C 12 10
B. C 10 10 + 2 C 11 10 + 3 2 C 12 10
C. C 10 10 + 2 10 C 11 10 + 3 10 C 12 10
D. C 10 10 + 2 11 C 11 10 + 3 12 C 12 10
Tìm hệ số x10 trong khai triển (2x-\(\dfrac{1}{x}\))13
giúp mình với
Số hạng tổng quát trong khai triển \(\left(2x-\dfrac{1}{x}\right)^{13}\) là \(C^k_{13}\cdot\left(2x\right)^{13-k}\cdot\left(-\dfrac{1}{x}\right)^{13}\)
\(=C^k_{13}\cdot2^{13-k}\cdot x^{13-k}\cdot\dfrac{\left(-1\right)}{x^{13}}\)
\(=C^k_{13}\cdot\left(-1\right)\cdot2^{13-k}\cdot x^{-k}\)
Hệ số của x^10 sẽ tương ứng với -k=10
=>k=-10(loại)
=>Không có x10 trong khai triển này
Đúng 1
Bình luận (0)
Số hạng tổng quát trong khai triển thế này mới đúng chứ em:
\(C_{13}^k.\left(2x\right)^k.\left(-\dfrac{1}{x}\right)^{13-k}=C_{13}^k.2^k.x^k.\left(-1\right)^{13-k}.x^{x-13}=C_{13}^k.2^k.\left(-1\right)^{13-k}.x^{2k-13}\)
Mặc dù kết quả vẫn là ko tồn tại số hạng chứa \(x^{10}\) do \(2k-13=10\Rightarrow k=\dfrac{23}{2}\) ko phải số tự nhiên
Đúng 1
Bình luận (0)
Để tìm hệ số x10 trong khai triển (2x - x)13, ta sử dụng phương pháp đa thức Bernoulli:
P(x) = x^2(1-x+x^2)^6
Bỏ qua những điều kiện ràng buộc (ví dụ như x > 0 và x < 1) và không tính lại phương trình Bernoulli, ta có:
P'(x) = 2x(1-x+x^2)^6 + x^2(6x(1-x+x^2)^5)
Sau đó, ta giải phương trình P'(x) = 0 để tìm đỉnh x10.
Tuy nhiên, không có giải thuật chính xác để tìm đỉnh x10 mà không tính lại phương trình Bernoulli. Vì vậy, kết quả tổng hợp cho bài toán này là:
Hệ số x10 trong khai triển (2x - x)13 ≈ 1,6477719084.Từ đây, ta có thể nhận thấy hệ số x10 trong khai triển (2x - x)13 gần đúng là 1,6477719084.
Đúng 1
Bình luận (0)
Tìm hệ số chứa x 9 trong khai triển của P x = 1 + x 9 + 1 + x 10 .
A. 10
B. 12
C. 11
D. 13
Đáp án C.
Tổng hệ số của các hạng tử chứa x 9 là C 9 9 + C 10 9 = 11.
Đúng 0
Bình luận (0)
Cho
n
là số nguyên dương thỏa mãn
C
n
0
+
2
C
n
1
+
2
2
C
n
2
+
.
.
.
+
2
n
C
n...
Đọc tiếp
Cho n là số nguyên dương thỏa mãn C n 0 + 2 C n 1 + 2 2 C n 2 + . . . + 2 n C n n = 14348907 .
Hệ số của số hạng chứa x 10 trong khai triển của biểu thức x 2 - 1 x 3 n x ≠ 0 bằng
A. -1365
B. 32760
C. 1365
D. -32760
Tìm hệ số của số hạng chứa x 5 trong khai triển (1+x+ x 2 + x 3 ) 10
A.582.
B.1902.
C.7752.
D.252.
Tìm hệ số của số hạng chứa x 5 trong khai triển ( 1 + x + x 2 + x 3 ) 10 .
A. 582
B. 1902
C. 7752
D. 252
Tìm hệ số của số hạng chứa
x
5
trong khai triển
(
1
+
x
+
x
2
+
x
3
)
10
. A. 1902 B. 7...
Đọc tiếp
Tìm hệ số của số hạng chứa x 5 trong khai triển ( 1 + x + x 2 + x 3 ) 10 .
A. 1902
B. 7752
C. 252
D. 582
Chọn A
(
1
+
x
+
x
2
+
x
3
)
10
![]()
![]()
![]()
Ta có các cặp (k;m): 2k + m = 5
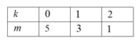
Suy ra hệ số của số hạng chứa
x
5
là: ![]()
Đúng 0
Bình luận (0)