Cho điểm O là trung điểm của đoạn thẳng AB, Trên cùng một nửa mặt phẳng bờ chứa cạnh AB, vẽ các tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm C ( C ≠ A ), qua O kẻ đường thằng vuông góc với OC cắt tia By tại D
a. Chứng minh : AB2 = 4AC . BD
b. Kẻ OM ⊥ CD tại M. Chứng minh : CO là tia phân giác của \(\widehat{ACD}\) và AC = MC
c. Tia BM cắt tia Ax tại N. Chứng minh : C là trung điểm của AN
d. Kẻ MH ⊥ AB tại H. Chứng minh : Các đường thẳng AD, BC, MH dồng quy
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz, Dt ở cùng phía đối với mặt phẳng (ABCD), song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz và Dt tại A’, B’, C’ và D’.
a) Chứng minh: mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt)
b) Gọi I = AC ∩ BD, J = A’C’ ∩ B’D’. Chứng minh: IJ song song với AA’.
c) Cho AA’ = a, BB’ = b, CC’ = c. Hãy tính DD’.
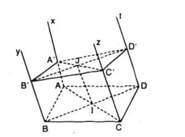
a) Do ABCD là hình bình hành, nên AB // DC
=> AB // (Cz, Dt) (1)
Theo giả thiết Ax // Dt nên Ax // (Cz, Dt) (2)
Từ (1) và (2) suy ra: (Ax, By) // (Cz, Dt)
b) Mặt phẳng β cắt 2 mặt phẳng song song ( Ax, By), (Cz, Dt) theo hai giao tuyến là A’B’và C’D’ nên A’B’// C’D’. (3)
Chứng minh tương tự (Ax, Dt) song song với (By,Cz).Và mặt phẳng β cắt 2 mặt phẳng song song (Ax, Dt), (By, Cz) theo hai giao tuyến là A’D’và B’C’ nên A’D’// B’C’ (4)
Từ (3) và (4) suy ra: tứ giác A’B’C’D’ là hình bình hành.
=> J là trung điểm của A’C’ ( tính chất hình bình hành).
Tứ giác AA’C’C là hình thang vì có: AA’ // CC’ ( giả thiết). Lại có, I và J lần lượt là trung điểm của AC và A’C’ nên IJ là đường trung bình của hình thang
=> IJ// AA’// CC’ ( đpcm).
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’
=> DD’ = AA’ + CC’ – BB’ = a + c – b
cho \(ax^3=by^3=cz^3;\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\). chứng minh \(\sqrt[3]{ax^2+by^2+cz^2}=\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\)
Bài này hình như có lần làm rồi :))
Đặt `ax^3=by^3=cz^3=k^3`
`=>a=k^3/x^3,b=k^3/y^3,c=k^3/z^3`
`=>root{3}{a}+root{3}{b}+root{3}{c}=k/x+k/y+k/z=k(1/x+1/y+1/z)=k(1)`
`**:ax^2+by^2+cz^2=(ax^3)/x+(by^3)/y+(cz^3)/z=k^3/x+k^3/y+k^3/z=k^3(1/x+1/y+1/z)=k^3`
`=>root{3}{ax^2+by^2+cz^2}=k(2)`
`(1)(2)=>ĐPCM`
Cho hình vẽ biết Cz//Ax,góc c=30°,góc ACB=110° a)chứng minh Ax//By,Cz//By b)tính góc CBy c)tính số đo góc acd
Giúp tui với mn ơi cần gấp lắm ròi :<
Cho hình vẽ:
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
Từ bốn đỉnh của hình bình hành ABCD vẽ bốn nửa đường thẳng song song cùng chiều Ax, By, Cz và Dt sao cho chúng cắt mặt phẳng (ABCD). Một mặt phẳng (α) cắt bốn nửa đường thẳng theo thứ tự nói trên tại A’, B’, C’ và D’.
a) Chứng minh rằng (Ax,By) // (Cz,Dt) và (Ax,Dt) // (By,Cz)
b) Tứ giác A'B'C'D' là hình gì?
c) Chứng minh AA′ + CC′ = BB′ + DD′.
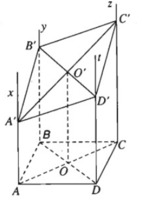
a) Ta có:
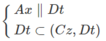
⇒ Ax // (Cz,Dt)
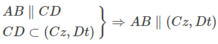
Từ Ax, AB ⊂ (Ax,By) suy ra (Ax, By) // (Cz, Dt)
Tương tự ta có (Ax, Dt) // (By,Cz)
b)
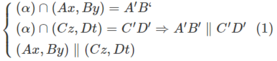
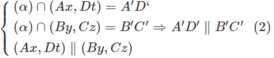
Từ (1) và (2) suy ra tứ giác A’B’C’D’ là hình bình hành.
c) Gọi O, O’ lần lượt là tâm các hình bình hành ABCD, A’B’C’D’. Dễ thấy OO’ là đường trung bình của hình thang AA’, suy ra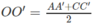 
Tương tự ta có:
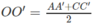
(2,0 điểm) Cho hình vẽ, biết $Cz // Ax;$ $\widehat{C}=30^{\circ} ; \widehat{A C B}=110^{\circ}$.
a) Chứng minh rằng: ${Ax} / / {By}$ và ${Cz} / / {By}$;
b) Tính số đo góc $\widehat{C B y}$;
a/
\(Ax\perp m\left(gt\right);By\perp m\left(gt\right)\) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
b/
\(\widehat{BCz}=\widehat{ACB}-\widehat{C}=110^o-30^o=80^o\)
Ta có
Cz//By (cmt) \(\Rightarrow\widehat{BCz}=\widehat{CBy}=80^o\) (góc so le trong)
c/
\(CD\perp Ax\left(gt\right)\Rightarrow\widehat{ADC}=90^o\)
Cz//Ax (gt) \(\Rightarrow\widehat{A}=\widehat{C}=30^o\) (Góc so le trong)
Xét tg vuông ACD có
\(\widehat{ACD}=\widehat{ADC}-\widehat{A}=90^o-30^o=60^o\)
A) Ax⊥m(gt);By⊥m(gt) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
Cho △ABC có 3 góc nhọn. Gọi D là trung điểm của BC trên tia đối của tia DA lấy điểm E sao cho AD = AE.
a) Chứng minh △ABD và △ECD.
b) Chứng minh AB // CE.
c) Kẻ DH ⊥ AC tại H, DK ⊥ BE tại K. Chứng minh D à trung điểm của HK.
a/ △ABD và △ECD có:
AD=DE (gt)
BD=DC (D là trung điểm)
\(\widehat{BDA}=\widehat{CDE}\) (đối đỉnh)
➜ △ABD = △ECD (c.g.c)
b/ Từ chứng minh trên, ta suy ra:
\(\widehat{ABD}=\widehat{DCE}\) (hai góc tương ứng)
vì hai góc trên nằm ở vị trí so le trong nên AB//CE
c/❄△BDE và △ADC có:
\(\widehat{BDE}=\widehat{ADC}\) (đối đỉnh)
AD=DE (gt)
BD=DC (D là trung điểm)
➜△BDE=△ADC (c.g.c)
➜\(\widehat{EBD}=\widehat{ACD}\) (2 góc tương ứng)
❄△BDK và △ADH có:
\(\widehat{EBD}=\widehat{ACD}\) (△BDE=△ADC)
BD=DC (D là trung điểm)
\(\widehat{BDK}=\widehat{CDH}\) (đối đỉnh) ➜ △BDK =△ADH (g.c.g)(vì câu này không thể chứng minh theo các hướng khác nên mình đành làm cách này) ➜ KD=HD (2 cạnh tương ứng) ➜ D là trung đểm của KH
cho góc nhọn xBy, Bz là tia phân giác . từ điểm A bất kì trên Bx, kẻ AH⊥By (H∈By), kẻ AD⊥Bz (D∈Bz). gọi O là trung điểm của AB
a/ chứng minh OD⊥AH
b/ tiếp tuyến tại A của đường tròn (O), đường kính AB cắt By tại C, cắt Bz tại E. chứng minh tức giác HDEC nội tiếp
Cho ΔABC cân tại A, biết AB = 5cm, BC = 6cm. Gọi H là trung điểm của BC.
a) Chứng minh: ΔABH = ΔACH
b) Chứng minh: AH ⊥ BC
c) Tính AH
d) Kẻ HE ⊥ AB (E ∈ AB), HK ⊥ AC (K ∈ AC). Chứng minh: HE = HK
e) Chứng minh: EK // BC
Ai giúp mik vs !!
![•◇[ Shia_chan ]◇•](https://hoc24.vn/images/avt/avt151087886_256by256.jpg)
