mọi ngườ giúp e câu này với ạ
cho hai tập hợp H={\(x\in R,1\le\left|x-2\right|< 3\)} , K=(0;3]\(\cup\left(\frac{7}{2};+\infty\right)\)
tìm H\(\cap K\)
Những câu hỏi liên quan
cho hai tập hợp H={\(x\in R,1\le\left|x-2\right|< 3\) } , K=(0;3]\(\cup\left(\frac{7}{2};+\infty\right)\)
Tìm \(H\cap K\)
mọi người giúp e với ạ
Bài 1. (2 điểm)
a) Liệt kê các phần tử của tập hợp $A=\left\{ x\in \mathbb{Z} \, \Big| \, 2{{x}^{2}}+3x+1=0 \right\}$.
b) Cho hai tập hợp $A=\left\{ x\in \mathbb{R} \, \Big| \, |x|>4 \right\}$ và $B=\left\{ x\in \mathbb{R} \, \Big| \, -5\le x-1<5 \right\}$. Xác định tập $X=B\backslash A$.
Xem thêm câu trả lời
Cho hai tập hợp:
\(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\}\)
\(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} \)
Tìm \(A\,{\rm{\backslash }}\,B\) và \(B\,{\rm{\backslash }}\,A\).
Ta có: \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\} = \{ - 2; - 1;0;1;2;3\} \)
Và \(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} = \{ - 2;3\} \)
Khi đó:
Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các phần tử thuộc A mà không thuộc B. Vậy\(A\,{\rm{\backslash }}\,B = \{ - 1;0;1;2\} \).
Tập hợp \(B\,{\rm{\backslash }}\,A\) gồm các phần tử thuộc B mà không thuộc A. Vậy \(B\,{\rm{\backslash }}\,A = \emptyset \)
Đúng 0
Bình luận (0)
Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:
a) \(\left\{ {x \in \mathbb{R}|\; - 2\pi < x \le 2\pi } \right\}\)
b) \(\left\{ {x \in \mathbb{R}|\;\left| x \right| \le \sqrt 3 } \right\}\)
c) \(\{ x \in \mathbb{R}|\;x < 0\} \)
d) \(\left\{ {x \in \mathbb{R}|\;1 - 3x \le 0} \right\}\)
a) Nửa khoảng \(\left( {\left. { - 2\pi ;2\pi } \right]} \right.\)
b) \(\left\{ {x \in \mathbb{R}|\;\left| x \right| \le \sqrt 3 } \right\} = \left\{ {x \in \mathbb{R}|\; - \sqrt 3 \le x \le \sqrt 3 } \right\}\)
Đoạn \(\left[ {\left. { - \sqrt 3 ;\sqrt 3 } \right]} \right.\)
c) Khoảng \(\left( { - \infty ;0} \right)\)
d) \(\left\{ {x \in \mathbb{R}|\;1 - 3x \le 0} \right\} = \left\{ {x \in \mathbb{R}|\;x \ge \frac{1}{3}} \right\}\)
Nửa khoảng \(\left. {\left[ {\frac{1}{3}; + \infty } \right.} \right)\)
Đúng 0
Bình luận (0)
Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:a) left{ {x in mathbb{R}|; - 2 x 3} right}b) left{ {x in mathbb{R}|;1 le x le 10} right}c) left{ {x in mathbb{R}|; - 5 x le sqrt 3 } right}d) left{ {x in mathbb{R}|;pi le x 4} right}e) { x in mathbb{R}|;x frac{1}{4}} g) { x in mathbb{R}|;x ge frac{pi }{2}}
Đọc tiếp
Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:
a) \(\left\{ {x \in \mathbb{R}|\; - 2 < x < 3} \right\}\)
b) \(\left\{ {x \in \mathbb{R}|\;1 \le x \le 10} \right\}\)
c) \(\left\{ {x \in \mathbb{R}|\; - 5 < x \le \sqrt 3 } \right\}\)
d) \(\left\{ {x \in \mathbb{R}|\;\pi \le x < 4} \right\}\)
e) \(\{ x \in \mathbb{R}|\;x < \frac{1}{4}\} \)
g) \(\{ x \in \mathbb{R}|\;x \ge \frac{\pi }{2}\} \)
a) Khoảng \(\left( { - 2;3} \right)\)
b) Đoạn \(\left[ {1;10} \right]\)
c) Nửa khoảng \(\left( {\left. { - 5;\sqrt 3 } \right]} \right.\)
d) Nửa khoảng \(\left. {\left[ {\pi ;4} \right.} \right)\)
e) Khoảng \(\left( { - \infty ;\frac{1}{4}} \right)\)
g) Nửa khoảng \(\left[ {\left. {\frac{\pi }{2}; + \infty } \right)} \right.\)
Đúng 0
Bình luận (0)
Cho hàm số \(f\left(x\right)\) có đồ thị \(f'\left(x\right)=\left(e^x-1\right)\left(x^2-x-2\right)\)với mọi \(x\in R\).Số điểm cực tiểu của hàm số đã cho là
A. 0.
B. 1.
C. 2.
D. 3
\(f'\left(x\right)=0\) có 3 nghiệm \(x=-1;0;2\)
Dấu của \(f'\left(x\right)\) trên trục số:
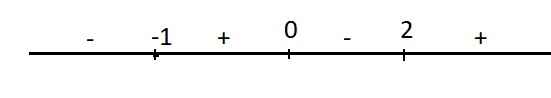
Ta thấy có 2 lần \(f'\left(x\right)\) đổi dấu từ âm sang dương nên hàm có 2 cực tiểu
Đúng 2
Bình luận (0)
hãy liệt kê các phần tử của tập hợp sau:
A=\(\left\{x\in Z|\left(x+1\right)\left(3x^2-10x+3\right)=0\right\}\)
B=\(\left\{2k+1|k\in Z;\left|k\right|\le2\right\}\)
m.n giúp mk bài này với ạ. thank m.n
A={-1} (vì x thuộc Z)
B={-3,-1,1,3,5} (thay k lần lượt =-2,-1,0,1,2 vào 2k+1)
Đúng 0
Bình luận (0)
Bài 1:Cho mệnh đề:∀x∈R,x+30(1). Hãy xét tính đúng sai (có giải thích) và lập mệnh đề phủ định của mệnh đề (1)
Bài 2:
a)CM định lý sau bằng phản chứng : Với mọi số tự nhiên n, nếu 5n+3 chia hết cho 3 thì n chia hết cho 3
b)Hãy quy tròn số gần đúng của sqrt{10} đến hàng phần nghìn
Bài 3:Hãy viết tập hợp sau dưới dạng liệt kê các phần tử
A{x∈R|x^3-7x^2+2x+160}
Câu 4: Cho các tập hợp B{x∈R|x≤3}
C{x∈R|-2≤x≤4}...
Đọc tiếp
Bài 1:Cho mệnh đề:"∀x∈R,x+3>0"(1). Hãy xét tính đúng sai (có giải thích) và lập mệnh đề phủ định của mệnh đề (1)
Bài 2:
a)CM định lý sau bằng phản chứng :" Với mọi số tự nhiên n, nếu 5n+3 chia hết cho 3 thì n chia hết cho 3 "
b)Hãy quy tròn số gần đúng của \(\sqrt{10}\) đến hàng phần nghìn
Bài 3:Hãy viết tập hợp sau dưới dạng liệt kê các phần tử
A={x∈R|\(x^3-7x^2+2x+16=0\)}
Câu 4: Cho các tập hợp B={x∈R|x≤3}
C={x∈R|-2≤x≤4}
a)Hãy viết các tập hợp B,C dưới dạng khoảng, nửa khoảng hoặc nửa đoạn
b)Tìm B giao C, B hợp C, B\C , CRC
c)Cho tập hợp E={x∈R| |2x-1| >1}. Tìm CR (E giao C)
Câu 5:Cho tập hợp D={x∈R| x+\(\sqrt{2x-1}\) =2(x-3)2. Hãy viết tập hợp D dưới dạng liệt kê các phần tử
Cho hai tập hợp \(A=\left(0;+\infty\right)\) và \(B=\left\{x\in R|mx^2-4x+m-3=0\right\}\). Tìm m để B có đúng 2 tập hợp con và \(B\subset A\)
\(mx^2-4x+m-3=0\left(1\right)\)
Để tập hợp B có đúng 2 tập con và \(B\subset A\) thì \(\left(1\right)\) có 2 nghiệm phân biệt cùng dương
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\P>0\\S>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4-m\left(m-3\right)>0\\\dfrac{m-3}{m}>0\\\dfrac{4}{m}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-4< 0\\m< 0\cup m>3\\m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 4\\m< 0\cup m>3\\m>0\end{matrix}\right.\)
\(\Leftrightarrow3< m< 4\)
Đúng 0
Bình luận (0)
Ta có:
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}\)
+) \(\overrightarrow{BG}=\dfrac{1}{3}\left(\overrightarrow{BM}+\overrightarrow{BN}\right)=\dfrac{1}{3}\left(-\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CN}\right)\)
\(=\dfrac{1}{3}\left(-\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{DC}\right)=\dfrac{1}{3}\left(-\dfrac{13}{6}\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=-\dfrac{13}{18}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
=> \(\overrightarrow{AG}=\dfrac{5}{18}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
Mặt khác:
\(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}=\overrightarrow{AB}+k\overrightarrow{BC}=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
Để A, G, I thẳng hàng
=>\(\dfrac{\dfrac{5}{18}}{1-k}=\dfrac{\dfrac{1}{3}}{k}\Rightarrow k=\dfrac{6}{11}\)
Đúng 0
Bình luận (0)