Cho tam giác ABC qua điểm A vẽ đường thẳng a // BC và qua điểm B vẽ đường thẳng b // AC. Chứng tỏ a và b luôn luôn cắt nhau

Những câu hỏi liên quan
Cho tam giác ABC, qua điểm A vẽ đường thẳng a // BC và qua điểm B vẽ đường thẳng b // AC. Chứng minh rằng: a và luôn luôn cắt nhau
cho một tam giác ABC có AB=AC; O là trung điểm của BC.
a)chứng minh rằng: tam giác ABO bằng tam giác ACO
b)Qua điểm A vẽ đường thẳng song song với BC và qua điểm B vẽ đường thẳng vuông góc với BC, hai đường thẳng này cắt nhau tại K. Chứng minh rằng : AK=OC
GIÚP MÍNH CÂU b) NHA
Ta có hình vẽ sau:
a) Vì AB = AC => ΔABC cân => \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABO và ΔACO có:
AO: cạnh cung
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
OB = OC (gt)
=> ΔABO = ΔACO (đpcm)
b) Vì AK // BC(gt) => \(\widehat{KAB}=\widehat{ABO}\) (so le trong)
Mà \(\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{KAB}=\widehat{ACB}\) (*)
Vì ΔABO = ΔACO (ý a) => \(\widehat{A_1}=\widehat{A_2}\)
mà \(\widehat{A_1}=\widehat{ABK}\) (so le trong do AK // BC)
=> \(\widehat{A_2}=\widehat{ABK}\) (**)
Xét ΔABK và ΔACO có:
\(\widehat{KAB}=\widehat{ACB}\) (*)
AB = AC (gt)
\(\widehat{A_2}=\widehat{ABK}\) (**)
=> ΔABK = ΔACO (g.c.g)
=> AK = OC (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Qua A vẽ đường thẳng a//BC. Qua B vẽ đường thẳng b//AC và qua C vẽ đường thẳng c//AB. Các đường thẳng b và c cắt nhau tại A' và cắt đường thẳng a lần lượt tại C' và B'. Chứng minh rằng: ∆ABC và ∆A'B'C' có cùng một trọng tâm
cho tam giác ABC. Qua điểm A vẽ đường thẳng A song song với BC, qua điểm B vẽ đường thẳng b song song với AC. Hỏi:
a) Vẽ được mấy đường thẳng a, mấy đường thẳng b. Vì sao?
b)Đường thẳng a và b có cắt nhau không?Vì sao?
Giải giúp mk nha
Cho 3 điểm ko thẳng hàng A,B,C. Qua A vẽ đường thẳng a //BC; qua C vẽ đường thẳng b //AB; qua a và b cắt nhau tại D. Chứng tỏ góc BAD = BCD, ABC = ADC?
Giúp mik nha
Cho tam giác ABC có AB 6cm,AC 8cm và BC 10cm. Lấy điểm B trên AB sao cho . Qua B vẽ đường thẳng song song với BC và cắt AC tại C.a) Tính AC.b) Qua C vẽ đường thẳng song song với AB và cắt BC tại D. Tính BD,BC.c) Tính và so sánh các tỉ số: frac{{AB}}{{AB}},frac{{AC}}{{AC}} và frac{{BC}}{{BC}}.
Đọc tiếp
Cho tam giác \(ABC\) có \(AB = 6cm,AC = 8cm\) và \(BC = 10cm\). Lấy điểm \(B'\) trên \(AB\) sao cho . Qua \(B'\) vẽ đường thẳng song song với \(BC\) và cắt \(AC\) tại \(C'\).
a) Tính \(AC'\).
b) Qua \(C'\) vẽ đường thẳng song song với \(AB\) và cắt \(BC\) tại \(D\). Tính \(BD,B'C'\).
c) Tính và so sánh các tỉ số: \(\frac{{AB'}}{{AB}},\frac{{AC'}}{{AC}}\) và \(\frac{{B'C'}}{{BC}}\).
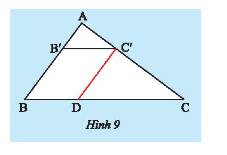
a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
Đúng 1
Bình luận (0)
cho tam giác ABC qua A vẽ đường thẳng a //BC qua B vẽ đường thẳng b//AC qua C vẽ đường thẳng c//AB.abc,lần lượt cắt nhau tại PQR hãy so sánh các góc của tam giác PQR và các góc của tam giác ABC
cho tam giác ABC qua A vẽ đường thẳng a //BC qua B vẽ đường thẳng b//AC qua C vẽ đường thẳng c//AB.abc,lần lượt cắt nhau tại PQR hãy so sánh các góc của tam giác PQR và các góc của tam giác ABC
Cho tam giác ABC. Qua A vẽ đường thẳng xy//BC. Từ điểm M trên cạnh BC vẽ các đường thẳng song song với AB và AC, chúng cắt xy theo thứ tự tại D và E. Chứng minh rằng: a/ EC đi qua chung điểm của AM b/ Ba đường thẳng AM, BD, CE đồng quy.
Xem chi tiết
Giải thích các bước giải:
a.Ta có xy//BC,MD//AB��//��,��//��
→AD//BM,AB//DM→ˆBMA=ˆMAD,ˆBAM=ˆAMD→��//��,��//��→���^=���^,���^=���^
Mà ΔABM,ΔMDAΔ���,Δ��� chung cạnh AM��
→ΔABM=ΔMDA(g.c.g)→Δ���=Δ���(�.�.�)
→AD=BM,MD=AB→��=��,��=��
Tương tự chứng minh được AE=MC,ME=AC��=��,��=��
→DE=DA+AE=BM+MC=BC→��=��+��=��+��=��
→ΔABC=ΔMDE(c.c.c)→Δ���=Δ���(�.�.�)
b.Gọi AM∩BD=I��∩��=�
→ˆIAD=ˆIMB,ˆIDA=ˆIBM(AD//BM)→���^=���^,���^=���^(��//��)
Mà AD=BM��=��
→ΔIAD=ΔIMB(g.c.g)→Δ���=Δ���(�.�.�)
→IA=IM,IB=ID→��=��,��=��
Lại có AE//CM→ˆEAI=ˆIMC��//��→���^=���^
Kết hợp AE=CM��=��
→ΔIAE=ΔIMC(c.g.c)→Δ���=Δ���(�.�.�)
→ˆAIE=ˆMIC→���^=���^
→ˆEIC=ˆAIE+ˆAIC=ˆMIC+ˆAIC=ˆAIM=180o→���^=���^+���^=���^+���^=���^=180�
→E,I,C→�,�,� thẳng hàng
→CE,AM,BD→��,��,�� đồng quy

Đúng 0
Bình luận (0)














