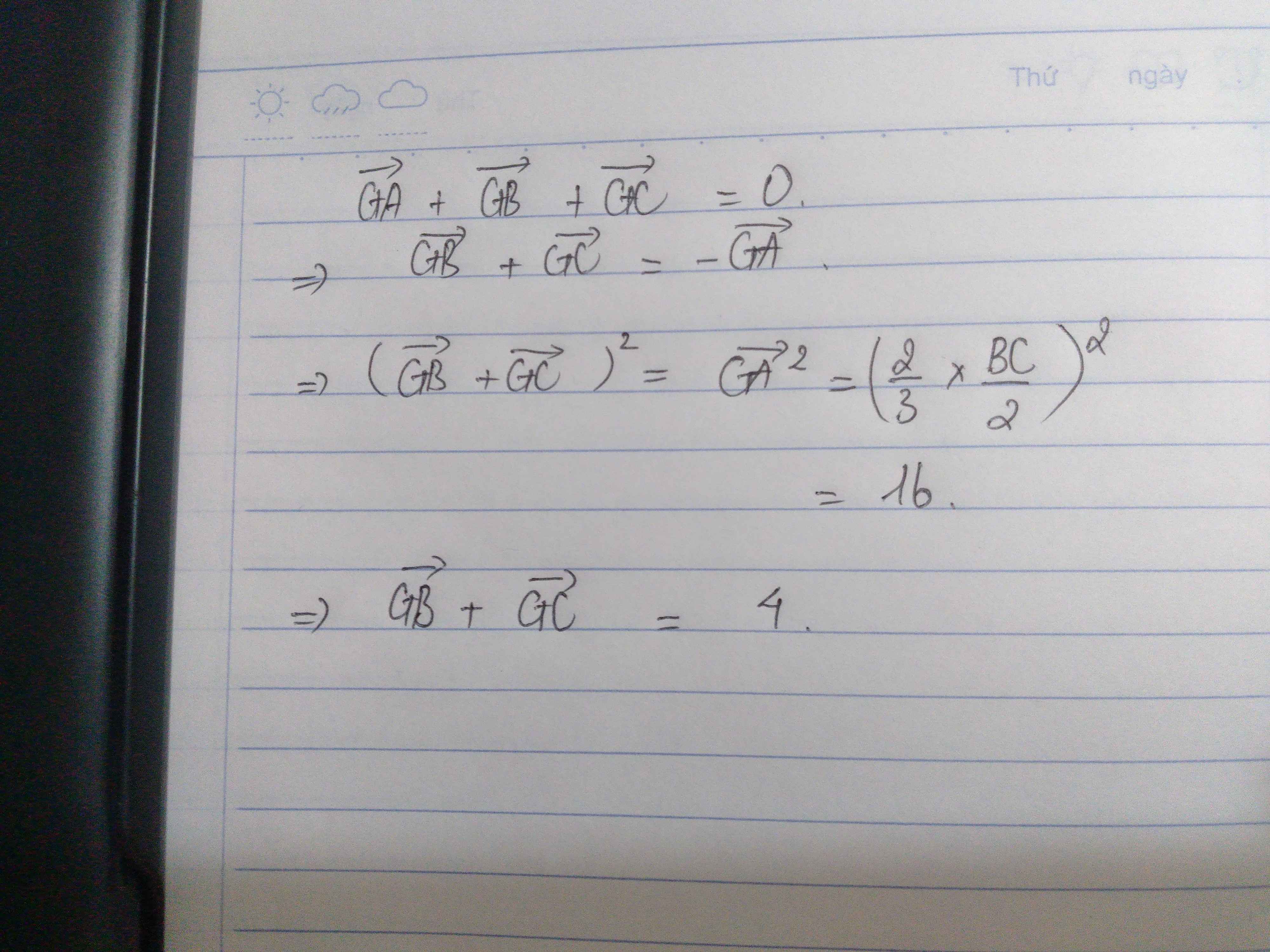Gọi G là trọng tâm của tam giác vuông ABC với cạnh huyền BC=12cm. Tổng hai vecto GB+ vecto GC có độ dài bằng bao nhiêu?

Những câu hỏi liên quan
Gọi G là trọng tâm tam giác ABC với cạnh huyền BC=12. Tổng hai vecto GB+GC bằng bao nhiêu Mọi người giúp mình giải câu này với
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC 12. Tính độ dài của vectơ
v
→
G
B
→
+
G
C
→
A.
v
→
2
B. ...
Đọc tiếp
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC= 12. Tính độ dài của vectơ v → = G B → + G C →
A. v → = 2
B. v → = 2 3
C. v → = 8
D. v → = 4
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC 12. Tính độ dài của vectơ
v
→
G
B
→
+
G
C
→
.
Đọc tiếp
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC = 12. Tính độ dài của vectơ v → = G B → + G C → .
![]()
![]()
![]()
![]()
Chọn D.
Gọi M là trung điểm của BC
Ta có ![]()
![]()
Mà AM = BC/ 2= 6 nên GA = 2/3. AM = 4
Đúng 0
Bình luận (0)
tam giác abc đều các cạnh là 2a có trọng tâm g khi đó vecto GA+GB-GC BẰNG
Gọi G là trọng tâm của tam giác ABC. Dựng vecto AD= vecto GC và vecto DE= vecto GB. Cmr vecto GE= vecto 0
Cho tam giác ABC có G là trọng tâm. Chọn khẳng định sai trong các khẳng định sau
A. vecto MA vecto MB vecto MC= 3 vecto MG
B. vecto GA vecto GB vecto GC= vecto 0
C. vecto GA= vecto GB= vecto GC
D. |vecto GA vecto GB vecto GC|=0
Xem chi tiết
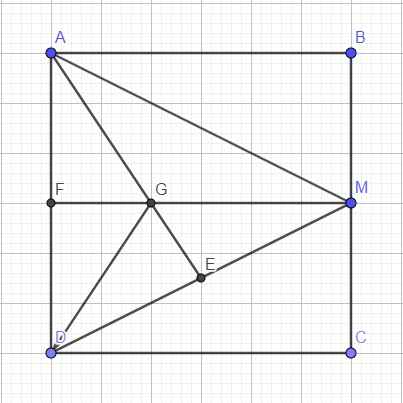
Cho hình vuông ABCD có độ dài cạnh bằng 6. Gọi M là trung điểm của BC và G là trọng tâm tam giác ADM. Tính độ dài vecto GD
\(\left\{{}\begin{matrix}AM=\sqrt{AB^2+BM^2}=3\sqrt{5}\\DM=\sqrt{CD^2+CM^2}=3\sqrt{5}\end{matrix}\right.\) \(\Rightarrow\) tam giác ADM cân tại M
Gọi F là trung điểm AD \(\Rightarrow ABMF\) là hình chữ nhật \(\Rightarrow MF=AB=6\)
Theo tính chất trọng tâm: \(GF=\dfrac{1}{3}MF=2\)
\(DF=\dfrac{1}{2}AD=3\)
Đặt \(T=\left|\overrightarrow{GD}\right|=\left|\overrightarrow{GF}+\overrightarrow{FD}\right|\)
\(\Rightarrow T^2=GF^2+FD^2+2\overrightarrow{GF}.\overrightarrow{DF}=GF^2+DF^2=2^2+3^2=13\)
\(\Rightarrow\left|\overrightarrow{GD}\right|=\sqrt{13}\)
Đúng 2
Bình luận (0)
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC=12.Tính độ dài của vecto \(\overrightarrow{v}=\overrightarrow{GB}+\overrightarrow{GC}\)
Gọi M là trung điểm BC
\(\Rightarrow\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GM}=2.\frac{1}{3}\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\left|\overrightarrow{v}\right|=\frac{2}{3}\left|\overrightarrow{AM}\right|\)
Mà \(AM=\frac{1}{2}BC=6\Rightarrow\left|\overrightarrow{v}\right|=4\)
Đúng 0
Bình luận (0)
giúp mình với các thần đồng !!
Cho G là trọng tâm tam giác ABC. CM:
a) vecto GA + vecto GB + vecto GC= vecto 0
b) vecto MA + vecto MB + vecto MC= 3 vecto MG ( với mọi M)
a: Gọi M là trung điểm của AB
Xét ΔABC có
G là trọng tâm
M là trung điểm của AB
Do đó: CG=2/3CM
=>CG=2GM
=>\(\overrightarrow{CG}=2\overrightarrow{GM}\)
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\)
\(=2\overrightarrow{GM}+\overrightarrow{GC}\)
\(=\overrightarrow{CG}+\overrightarrow{GC}=\overrightarrow{0}\)
b: \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
\(=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\)
\(=3\cdot\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=3\cdot\overrightarrow{MG}\)
Đúng 0
Bình luận (0)