cách tính một góc nhọn được tạo bởi mặt trời qua tháp khi biết một cạnh góc vuông
Những câu hỏi liên quan
Bài 7 Tia nắng chiếu qua ngọn một cái cây tạo với mặt đất một góc 52 độ. Tìm chiều cao của cây khi biết bóng của nó có chiều dài là 12m
Bài 8 Một người có mắt cách mặt đất 1.4m đứng cách tháp Eiffel 400m nhìn thấy đỉnh tháp với góc nâng 39 độ. Tính chiều cao của tháp (làm tròn đến mét).
7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)
Đúng 0
Bình luận (0)
a, Trên cùng một mặt phẳng vẽ aOb = 50 độ, aOc = 120 độ. Tính góc bOc?
b, Tính số góc nhọn được tạo bởi 2015 đường thẳng phân biệt cùng đi qua điểm O và không có hai đường thẳng nào vuông góc với nhau.
a) Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOb}< \widehat{aOc}\left(50^0< 120^0\right)\)
nên tia Ob nằm giữa hai tia Oa và Oc
\(\Leftrightarrow\widehat{aOb}+\widehat{bOc}=\widehat{aOc}\)
hay \(\widehat{bOc}=70^0\)
Đúng 3
Bình luận (0)
Hình 59 biểu diễn mặt cắt ngang của một con đê. Để đo góc nhọn MOP tạo bởi mặt nghiêng của con đê với phương nằm ngang, ngta dùng thước chữ T và đặt như hình vẽ (OA vuông góc với AB).Tính góc MOP, biết rằng dây dọi BC tạo với trục BA một góc ABC=32độ.
Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 34° và bóng của một tháp trên mặt đất dài 89m. Tính chiều cao của tháp (làm tròn đến mét).
Xét \(\Delta\) ABC vuông tại A
\(\tan\left(\widehat{C}\right)=\dfrac{AB}{AC}\)
\(\Leftrightarrow tan\left(34^0\right)=\dfrac{AB}{89}\)
\(\Leftrightarrow AB=60,03m\)
Đúng 1
Bình luận (0)
tính chiều cao của một cột tháp, biết rằng tia sáng của mặt trời tạo với phương nằm ngang của mặt đất một góc bằng 50o và bóng của nó trên mặt đất dài 96m.
Để đo góc nhọn MOP tạo bởi mặt nghiêng của con đê và phương nằm ngang, người ta dùng thước chữ T và đặt hình vẽ OA vuông góc AB. Tính góc MOP, biết rằng dây dọi BC tạo với trục BA một góc ABC= 32 độ
Cắt hình nón (N) đỉnh S cho trước bởi mặt phẳng qua trục của nó, ta được một tam giác vuông cân có cạnh huyền bằng
2
a
2
.
Biết BC là một dây cung đường tròn của đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng đáy của hình nón một góc
60
°
. Tính diện tích tam giác SBC.
Đọc tiếp
Cắt hình nón (N) đỉnh S cho trước bởi mặt phẳng qua trục của nó, ta được một tam giác vuông cân có cạnh huyền bằng 2 a 2 . Biết BC là một dây cung đường tròn của đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng đáy của hình nón một góc 60 ° . Tính diện tích tam giác SBC.
15 tháng 10 2023 lúc 23:08
1) Tính chiều cao của một cột đèn (làm tròn đến mét), biết bóng của của cột đèn được chiếu bởi ánh sáng mặt trời xuống đất dài và góc tạo bởi tia sáng với mặt đất là (hình vẽ dưới). 2) Cho ▲ ABC vuông tại A, đường cao AH .a) Giả sử HB4 cm và HC9 cm. Tính AB,AH , và số đo ABC (số đo góc làm tròn đến độ).b) Gọi E là hình chiếu của H trên AB , F là hình chiếu của H trên AC .Chứng minh AHEF và chứng minh AE.AB+AF.AC2EF^2 .c) Vẽ FK vuông góc vs BC (K ϵ BC)....
Đọc tiếp
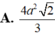
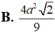
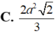
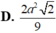
1) Tính chiều cao của một cột đèn (làm tròn đến mét), biết bóng của của cột đèn được chiếu bởi ánh sáng mặt trời xuống đất dài và góc tạo bởi tia sáng với mặt đất là (hình vẽ dưới).
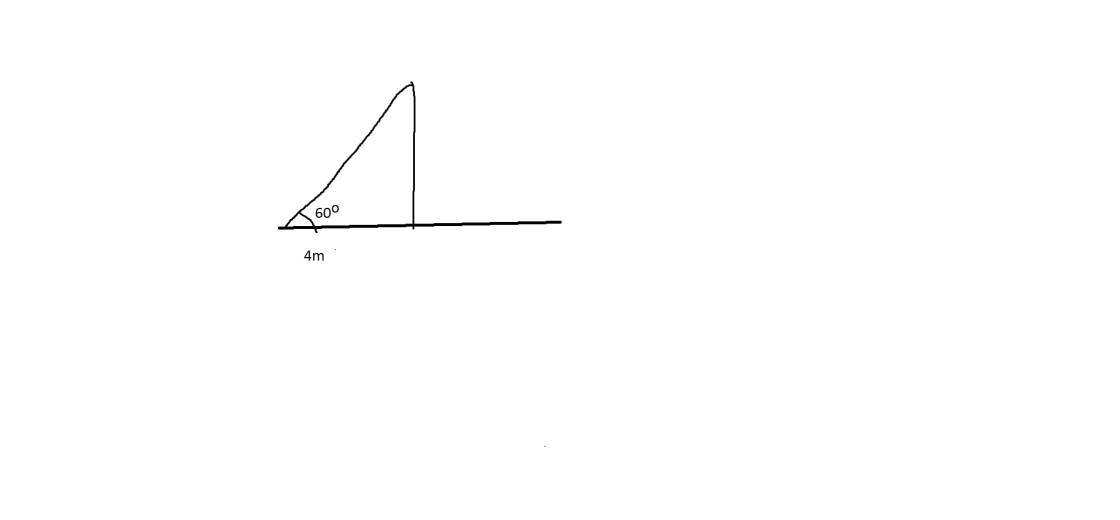
2) Cho ▲ ABC vuông tại A, đường cao AH .
a) Giả sử HB=4 cm và HC=9 cm. Tính AB,AH , và số đo ABC (số đo góc làm tròn đến độ).
b) Gọi E là hình chiếu của H trên AB , F là hình chiếu của H trên AC .
Chứng minh AH=EF và chứng minh \(AE.AB+AF.AC=2EF^2\) .
c) Vẽ FK vuông góc vs BC (K ϵ BC). Chứng minh \(KF=\dfrac{HC}{tanAHF+cotACB}\) .
Bài 2
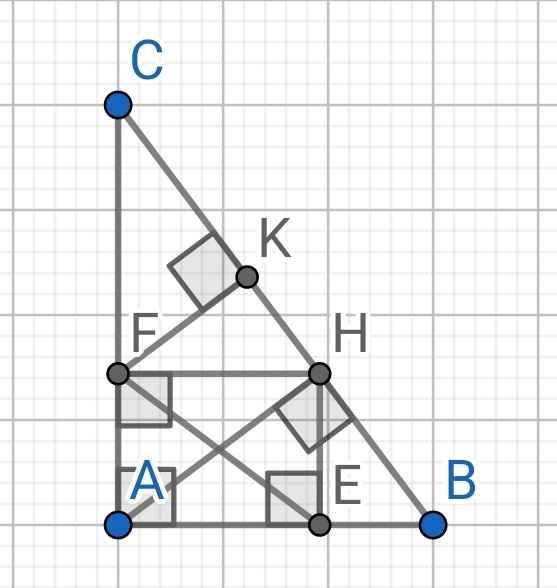a) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.HC
= 4.9
= 36
⇒ AH = 6 (cm)
BC = BH + HC
= 4 + 9 = 13 (cm)
∆ABC vuông tại A, AH là đường cao
⇒ AB² = BH.BC
= 4.13
= 52 (cm)
⇒ AB = 2√13 (cm)
⇒ cos ABC = AB/BC
= 2√13/13
⇒ ∠ABC ≈ 56⁰
b) ∆AHB vuông tại H, HE là đường cao
⇒ AH² = AE.AB (1)
∆AHC vuông tại H, HF là đường cao
⇒ AH² = AF.AC (2)
Từ (1) và (2) suy ra:
AE.AB + AF.AC = 2AH² (3)
Xét tứ giác AEHF có:
∠HFA = ∠FAE = ∠AEH = 90⁰ (gt)
⇒ AEHF là hình chữ nhật
⇒ AH = EF (4)
Từ (3) và (4) suy ra:
AE.AB + AF.AC = 2EF²
Đúng 1
Bình luận (0)
Bài 1
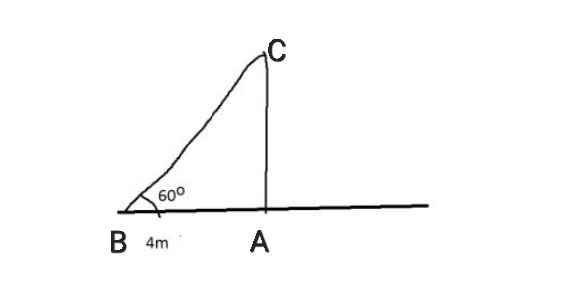Ta có:
tan B = AC/AB
⇒ AC = AB . tan B
= 4 . tan60⁰
= 4√3 (m)
≈ 7 (m)
Đúng 1
Bình luận (1)
Cho khối chóp tứ giác đều S.ABCD, gọi
α
mặt phẳng qua A và vuông góc SC. Biết rằng diện tích thiết diện tạo bởi
α
là hình chóp bằng nửa diện tích đáy ABCD. Tínhgóc
φ
tạo bởi cạnh bên SC và mặt đáy. A.
φ
arcsin
1
+
33
8
B.
φ
arcsin
33...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC.
Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính
góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = arcsin 1 + 33 8
B. φ = arcsin 33 − 1 8
C. φ = arcsin 1 + 29 8
D. φ = arcsin 29 − 1 8
