Xét tính đồng biến nghịch biến của hàm số sau:
y=f(x)=1/x-5 trên ( 5; + vô cực)
Ai giúp em với ạ dạng này em chưa làm qua
Những câu hỏi liên quan
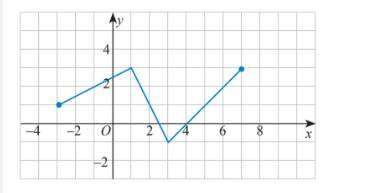
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
Đúng 0
Bình luận (1)
Xét tính đồng biến, nghịch biến của hàm số f(x) x − 3x + 5 trên khoảng (−
∞
; −5) và trên khoảng (−5; +
∞
). Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên (−
∞
; −5), đồng biến trên (−5; +
∞
). B. Hàm số đồng biến trên (−
∞
; −5), nghịch biến trên (−5; +
∞
). C. Hàm số nghịch biến trên các khoảng (−
∞
; −5) và (−5; +
∞...
Đọc tiếp
Xét tính đồng biến, nghịch biến của hàm số f(x) = x − 3x + 5 trên khoảng (− ∞ ; −5) và trên khoảng (−5; + ∞ ). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên (− ∞ ; −5), đồng biến trên (−5; + ∞ ).
B. Hàm số đồng biến trên (− ∞ ; −5), nghịch biến trên (−5; + ∞ ).
C. Hàm số nghịch biến trên các khoảng (− ∞ ; −5) và (−5; + ∞ ).
D. Hàm số đồng biến trên các khoảng (− ∞ ; −5) và (−5; + ∞ )
Xét tính đồng biến, nghịch biến của hàm số f(x)
x
2
−
4
x
+
5
trên khoảng (−
∞
; 2) và trên khoảng (2; +
∞
). Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên (−
∞
; 2), đồng biến trên (2; +
∞
). B. Hàm số đồng biến trên (−
∞
; 2), nghịch biến trên (2; +...
Đọc tiếp
Xét tính đồng biến, nghịch biến của hàm số f(x) = x 2 − 4 x + 5 trên khoảng (− ∞ ; 2) và trên khoảng (2; + ∞ ). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên (− ∞ ; 2), đồng biến trên (2; + ∞ ).
B. Hàm số đồng biến trên (− ∞ ; 2), nghịch biến trên (2; + ∞ ).
C. Hàm số nghịch biến trên các khoảng (− ∞ ; 2) và (2; + ∞ ).
D. Hàm số đồng biến trên các khoảng (− ∞ ; 2) và (2; + ∞ ).
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)
Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = (x + 1)/(x - 1) trên đoạn [3; 5].
y ' = - 2 x - 1 2 < 0 trên đoạn [3; 5]. Vậy hàm số nghịch biến trên đoạn [3; 5].
Khi đó trên đoạn [-3,5]: hàm số đạt giá trị lớn nhất tại x = 3 và giá trị lớn nhất bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất = 1.5.
Đúng 0
Bình luận (0)
Xét tính đồng biến và nghịch biến của hàm số \(y=f\left(x\right)=x^2+10x+9trên\left(-5;+\infty\right)\)
helpp mee, please
Đồ thị hàm số \(y=f\left(x\right)=x^2+10x+9\):
Dựa vào đồ thị ta thấy hàm số đồng biến trên \(\left(-5;+\infty\right)\).
P/s: Nên vẽ bảng biến thiên, bảng biến thiên trên máy tính nó vẽ mất công nên mới vẽ đồ thị thôi.
Đúng 0
Bình luận (0)
xét tính đồng biến nghịch biến của các hàm số trên
\(y=f\left(x\right)=x^2-2x+3\) trên khoảng \(_{\left(1;+\infty\right)}\)
y=f(x)=\(\sqrt{3-x}\) trên khoảng \(\left(-\infty;3\right)\)
Tìm khoảng đồng biến, nghịch biến của các hàm số sau:
y=x\(^4\)+4x2-3
y=x3+3x2+3x-2
a.
\(y'=4x^3+8x=4x\left(x^2+2\right)=0\Rightarrow x=0\)
Dấu của y':
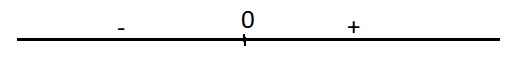
Hàm đồng biến trên \(\left(0;+\infty\right)\) và nghịch biến trên \(\left(-\infty;0\right)\)
b.
\(y'=3x^2+6x+3=3\left(x+1\right)^2\ge0\) ; \(\forall x\)
\(\Rightarrow\) Hàm đồng biến trên R
Đúng 0
Bình luận (0)
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y x2 trên đoạn [-3; 0];
b) y x+1x−1�+1�−1 trên đoạn [3; 5].
Đọc tiếp
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].