y ' = - 2 x - 1 2 < 0 trên đoạn [3; 5]. Vậy hàm số nghịch biến trên đoạn [3; 5].
Khi đó trên đoạn [-3,5]: hàm số đạt giá trị lớn nhất tại x = 3 và giá trị lớn nhất bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất = 1.5.
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = x 2 trên đoạn [-3; 0];
Cho hàm số y = f(x) nghịch biến trên ℝ và thỏa mãn [f(x) - x]f(x) = x 6 + 3 x 4 + 2 x 2 , ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
A. 4
B. -28
C. -3
D. 33
Cho hàm số y=f(x) liên tục trên [-3;2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-1;2]. Tính M + m.
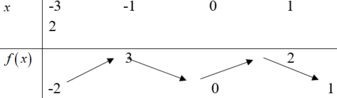
A. 3
B. 2
C. 1
D. 4
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m
A. -6
B. 2 3
C. 3 2
D. 6 5
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình dưới đây:
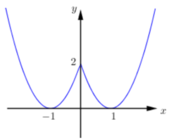
Xét các mệnh đề sau:
(I). Hàm số nghịch biến trên khoảng
(II). Hàm số đồng biến trên khoảng
(III). Hàm số có ba điểm cực trị
(IV). Hàm số có giá trị lớn nhất bằng 2.
Số mệnh đề đúng trong các mệnh đề trên là:
A. 4
B. 2
C. 3
D. 1
Gọi M, m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x = 4 x + x + 1 trên đoạn 1 ; 3 . Tính M - m
Kí hiệu M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;3]. Tính giá trị của M m .
Tính tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 + 3 - x ln x trên đoạn [1;2] là:
A. 
B. 
C. 
D. 
