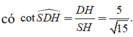Tứ giác ABCD là hình vuông khi và chỉ khi ABCD là hình chữ nhật và có AC vuông góc với BD (trong câu có mệnh đề đảo , mệnh đề kéo theo) . Hãy chứng minh P => Q là đúng và Q => P là đúng
Những câu hỏi liên quan
Xét hai mệnh đề:P: “Tứ giác ABCD là hình vuông”;Q: “Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau”.a) Phát biểu mệnh đề P Rightarrow Q và mệnh đề đảo của nó.b) Hai mệnh đề P và Q có tương đương không? Nếu có, sử dụng thuật ngữ “điều kiện cần và đủ” hoặc “khi và chỉ khi” để phát biểu định lí P Leftrightarrow Q theo hai cách khác nhau.
Đọc tiếp
Xét hai mệnh đề:
P: “Tứ giác ABCD là hình vuông”;
Q: “Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau”.
a) Phát biểu mệnh đề \(P \Rightarrow Q\) và mệnh đề đảo của nó.
b) Hai mệnh đề P và Q có tương đương không? Nếu có, sử dụng thuật ngữ “điều kiện cần và đủ” hoặc “khi và chỉ khi” để phát biểu định lí \(P \Leftrightarrow Q\) theo hai cách khác nhau.
a)
Mệnh đề \(P \Rightarrow Q\): “Nếu tứ giác ABCD là hình vuông thì nó là hình chữ nhật có hai đường chéo vuông góc với nhau”
Mệnh đề \(Q \Rightarrow P\): “Nếu tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau thì nó là hình vuông”
b)
Theo dấu hiệu nhận biết hình vuông, hai mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\) đều đúng. Do đó, P và Q là hai mệnh đề tương đương. Ta có thể phát biểu thành định lí như sau:
“Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau là điều kiện cần và đủ để nó là hình vuông”
Hoặc “Tứ giác ABCD là hình vuông khi và chỉ khi nó là hình chữ nhật có hai đường chéo vuông góc với nhau”
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Lập mệnh đề \(P \Rightarrow Q\) và xét tính đúng sai của mệnh đề đó với:
a) P: “Tứ giác ABCD là hình chữ nhật”, Q: “Tứ giác ABCD là hình bình hành”
b) P: “Tứ giác ABCD là hình thoi”, Q: “Tứ giác ABCD là hình vuông”
a) Mệnh đề \(P \Rightarrow Q\) là: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD là hình bình hành”
Đúng vì mỗi hình chữ nhật đều là hình bình hành.
b) Mệnh đề \(P \Rightarrow Q\) là: “Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD là hình vuông”
Sai vì hầu hết các hình thoi không là hình vuông
Đúng 0
Bình luận (0)
Phát biểu mệnh đề P
⇔
Q và xét tính đúng sai của nó với:P: Tứ giác ABCD là hình thoi và Q: Tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau A. Phát biểu: Tứ giác ABCD là hình thoi nếu tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau. Mệnh đề này đúng vì mệnh đề P Q,Q P đều đúng. B. Phát biểu: Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau. Mệnh đề này đúng vì mệnh đề P Q, Q P...
Đọc tiếp
Phát biểu mệnh đề P ⇔ Q và xét tính đúng sai của nó với:
P: "Tứ giác ABCD là hình thoi" và Q:" Tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau"
A. Phát biểu: "Tứ giác ABCD là hình thoi nếu tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau". Mệnh đề này đúng vì mệnh đề P => Q,Q => P đều đúng.
B. Phát biểu: "Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau". Mệnh đề này đúng vì mệnh đề P => Q, Q => P đều đúng.
C. Phát biểu: "Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau". Mệnh đề này sai vì mệnh đề P => Q, Q => P đều sai.
D. Phát biểu: "Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau". Mệnh đề này sai vì mệnh đề P => Q sai, Q => P đúng.
Phát biểu mệnh đề đảo của mỗi mệnh đề sau và xác định tính đúng sai của mệnh đề này.
P: “Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”;
Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”
Mệnh đề đảo của mệnh đề P: “Nếu số tự nhiên n chia hết cho 5 thì n có chữ số tận cùng là 5”;
Mệnh đề này sai. Chẳng hạn n = 10, chia hết cho 5 nhưng chữ số tận cùng là 0, không phải 5 .
Mệnh đề đảo của mệnh đề Q: “Nếu tứ giác ABCD có hai đường chéo bằng nhau thì tứ giác ABCD là hình chữ nhật"
Đúng 0
Bình luận (0)
Câu 23: Cho hai mệnh đề
P=”Tứ giác ABCD là hình thoi”, Q=”Tứ giác ABCD là hình vuông”. Khi đó mệnh đề nào sau đây đúng?
A. P => Q
B. Q => P
C. P <=> Q
D. Cả 3 đáp án trên sai
Hình vuông là trường hợp đặc biệt của hình thoi nên chọn Q ⇒ P
Đáp án B
Đúng 1
Bình luận (0)
Cho tứ giác ABCD. Xét tính đúng sai của mệnh đề P ⇒ Q với:
a) P = "ABCD là một hình vuông",
Q = "ABCD là một hình bình hành";
b) P = "ABCD là một hình thoi",
Q = "ABCD là một hình chữ nhật".
a) Mệnh đề P ⇒ Q là "Nếu ABCD là một hình vuông thì nó là một hình bình hành". Mệnh đề này đúng.
b) Mệnh đề P ⇒ Q là "Nếu ABCD là một hình thoi thì ABCD là một hình chữ nhật". Mệnh đề này sai.
Đúng 0
Bình luận (0)
Xét hai mệnh đề:
P: “Tứ giác ABCD là hình bình hành”.
Q: “Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường”.
a) Phát biểu mệnh đề \(P \Rightarrow Q\) và xét tính đúng sai của nó.
b) Phát biểu mệnh đề đảo của mệnh đề \(P \Rightarrow Q\).
a) Mệnh đề \(P \Rightarrow Q\): “Nếu tứ giác ABCD là hình bình hành thì nó có hai đường chéo cắt nhau tại trung điểm của mỗi đường”.
Mệnh đề này đúng vì “hai đường chéo cắt nhau tại trung điểm của mỗi đường” là tính chất của hình hình hành.
b) Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\), được phát biểu là: “Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường thì nó là hình bình hành”.
Đúng 0
Bình luận (0)
CÁC BẠN GIẢI JUP MIK VỚI !! :))Bài 1: Xét tính đúng sai của các mệnh đề sau:a) Phương trình có hai nghiệm phân biệt.b) 2k là số chẵn. (k là số nguyên bất kì)c) 211 – 1 chia hết cho 11.Bài 2: Cho tứ giác ABDC: Xét hai mệnh đềP: Tứ giác ABCD là hình vuông.Q: Tứ giác ABCD là hình chữ nhật có hai đường chéo bằng vuông góc với nhau.Hãy phát biểu mệnh đề P ↔ Q bằng hai cách khác nhau, xét tính đúng sai của các mệnh đề đó.Bài 3: Cho mệnh đề chứa biến P(n): n2 – 1 chia hết cho 4 với n là số nguyên. Xét...
Đọc tiếp
CÁC BẠN GIẢI JUP MIK VỚI !! :))
Bài 1: Xét tính đúng sai của các mệnh đề sau:
a) Phương trình có hai nghiệm phân biệt.
b) 2k là số chẵn. (k là số nguyên bất kì)
c) 211 – 1 chia hết cho 11.
Bài 2: Cho tứ giác ABDC: Xét hai mệnh đề
P: Tứ giác ABCD là hình vuông.
Q: Tứ giác ABCD là hình chữ nhật có hai đường chéo bằng vuông góc với nhau.
Hãy phát biểu mệnh đề P ↔ Q bằng hai cách khác nhau, xét tính đúng sai của các mệnh đề đó.
Bài 3: Cho mệnh đề chứa biến P(n): n2 – 1 chia hết cho 4 với n là số nguyên. Xét tính đúng sai của mệnh đề khi n = 5 và n = 2.
Bài 4: Nêu mệnh đề phủ định của các mệnh đề sau:
Bài 5: Xét tính đúng sai và nêu mệnh đề phủ định của các mệnh đề:
a) Tứ giác ABCD là hình chữ nhật.
b) 16 là số chính phương.
Bài 6: Cho tứ giác ABCD và hai mệnh đề:
P: Tổng 2 góc đối của tứ giác bằng 1800;
Q: Tứ giác nội tiếp được đường tròn.
Hãy phát biểu mệnh đề kéo theo P => Q và xét tính đúng sai của mệnh đề này.
Bài 7: Cho hai mệnh đề
P: 2k là số chẵn.
Q: k là số nguyên
Hãy phát biểu mệnh đề kéo theo và xét tính đúng sai của mệnh đề.
Bài 8: Hoàn thành mệnh đề đúng:
Tam giác ABC vuông tại A nếu và chỉ nếu ...................
- Viết lại mệnh đề dưới dạng một mệnh đề tương đương.
Bài 9: Xét tính đúng sai của các mệnh đề và viết mệnh đề phủ định của các mệnh đề.
Bài 10: Xét tính đúng sai của các suy luận sau: (mệnh đề kéo theo)
Bài 11: Phát biểu điều kiện cần và đủ để một:
Tam giác là tam giác cân.Tam giác là tam giác đều.Tam giác là tam giác vuông cân.Tam giác đồng dạng với tam giác khác cho trước.Phương trình bậc 2 có hai nghiệm phân biệt.Phương trình bậc 2 có nghiệm kép.Số tự nhiên chia hết cho 2; cho 3; cho 5; cho 6; cho 9 và cho 11.Bài 12: Chứng mình rằng: Với hai số dương a, b thì a + b ≥ 2√ab.
Bài 13: Xét tính đúng sai của mệnh đề:
Nếu một số tự nhiên chia hết cho 15 thì chia hết cho cả 3 và 5.
Bài 14: Phát biểu và chứng minh định lí sau:
a) n là số tự nhiên, n2 chia hết cho 3 thì n cũng chia hết cho 3.
b) n là số tự nhiên, n2 chia hết cho 6 thì n cũng chia hết cho cả 6; 3 và 2.
(Chứng minh bằng phản chứng)
Cho 2 mệnh đề: P: “Tứ giác là hình chữ nhật” và Q: “Tứ giác có hai đường chéo bằng nhau”. Hãy phát biểu và xét tính đúng sai của mệnh đề P tương đương Q?
\(P\Rightarrow Q\): Nếu tứ giác là hình chữ nhật thì đây là tứ giác có hai đường chéo bằng nhau
Đây là mệnh đề đúng
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy (ABCD). Gọi
φ
là góc giữa SD và mặt phẳng (ABCD). Mệnh đề nào sau đây đúng? A.cot
φ
5
15
B. cot
φ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy (ABCD). Gọi φ là góc giữa SD và mặt phẳng (ABCD). Mệnh đề nào sau đây đúng?
A.cot φ = 5 15
B. cot φ = 15 5
C. φ = 30 o
D. cot φ = 3 2
Chọn A
Gọi H là trung điểm AB
nên hình chiếu của SD trên (ABCD) là HD
Tam giác SAB đều cạnh a nên SH = a 3 2
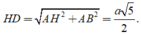
Tam giác vuông SHD
Đúng 1
Bình luận (0)