cho tam giác ABC. M,N,P lần lượt là trung điểm của AB,BC,CA trọng tâm G. CMR
a) AM+BN=1/2 AC
2) AM+BN+AP+BM=MC
3)AM+BN+CP=O
TẤT CẢ CÓ DẤU VÉC TƠ NHA
Những câu hỏi liên quan
Cho tam giác ABC .Gọi M , N, P lần lượt là trung điểm của BC , CA , AB và O là điểm bất kì .CMR
a, tổng các véc tơ AM +BN + CP bằng véc tơ 0
b, OA +OB+ OC = OM + ON +OP
cho tam giác ABC,có 3 đường trung tuyến lần lượt là CP,BN,ÂM,G là trọng tâm,lấy điểm D sao cho M là trung điểm của đoạn thẳng AD.Chứng minh AM<1/2(AB+AC)
cho tam giác ABC có trọng tâm G #đường trung tuyến AM : BN ; CP
CM 3(AM+BN+CP)<2(AB+BC+AC
Cho tam giác ABC đều với M; N ; P lần lượt là trung điểm của BC; CA; AB. Khẳng định nào sau đây đúng?
A. AM → + BN → + CP → = 0 →
B. MA → + BN → + CP → = 0 →
C. AM → + BN → = CP →
D. BN → + PC → = AM →
Cho Tam giác ABC với ba đường trung tuyến AM , BN , CP và trọng tâm G .Chứng minh rằng
a, AM < ( AB + AC )
b, ( AB + AC + CA ) < AM + BN + CP < AB + BC + CA
Tam giác ABC (hình vẽ) có ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác. Vẽ điểm D sao cho G là trung điểm của AD. Gọi E và F lần lượt là trung điểm của BD và BG.Điền số thích hợp vào ô trống: BM ....BC, GE ....AB, DF ....AC.
Đọc tiếp
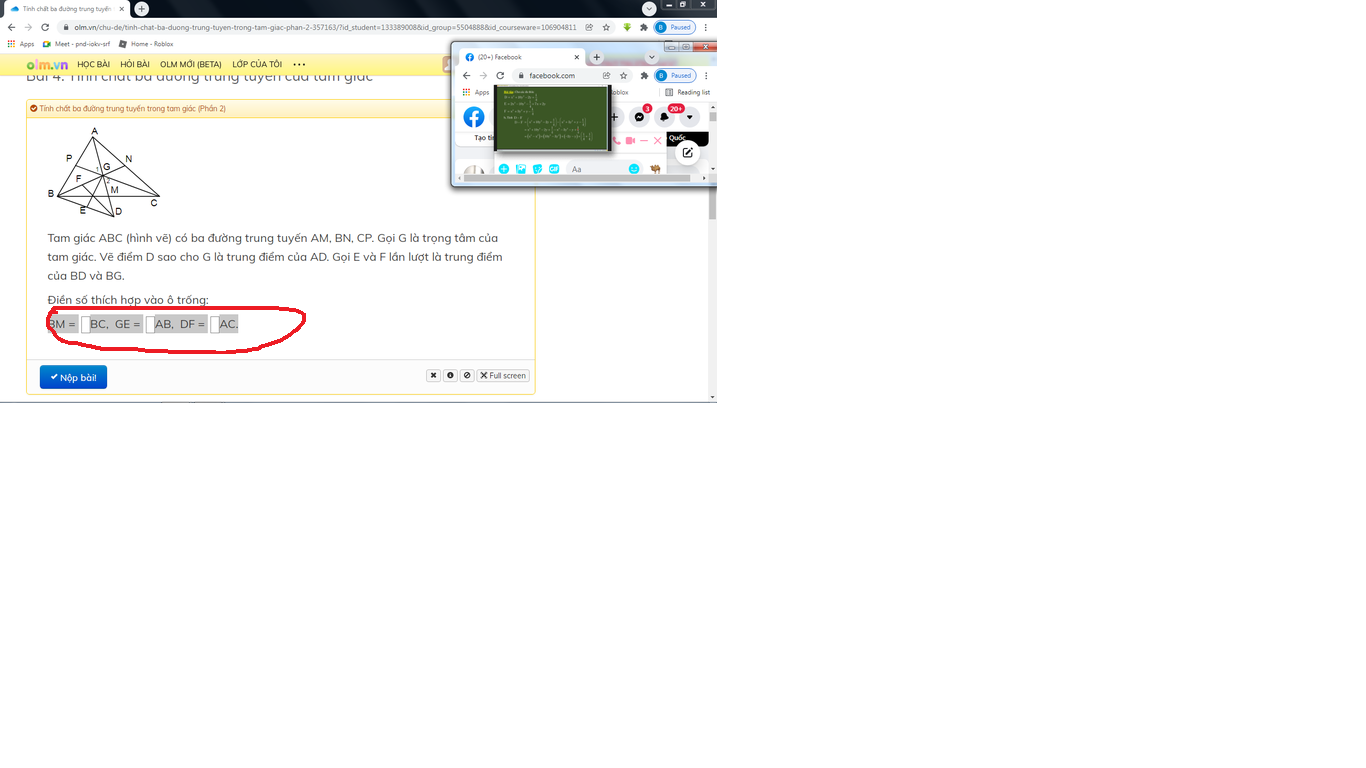
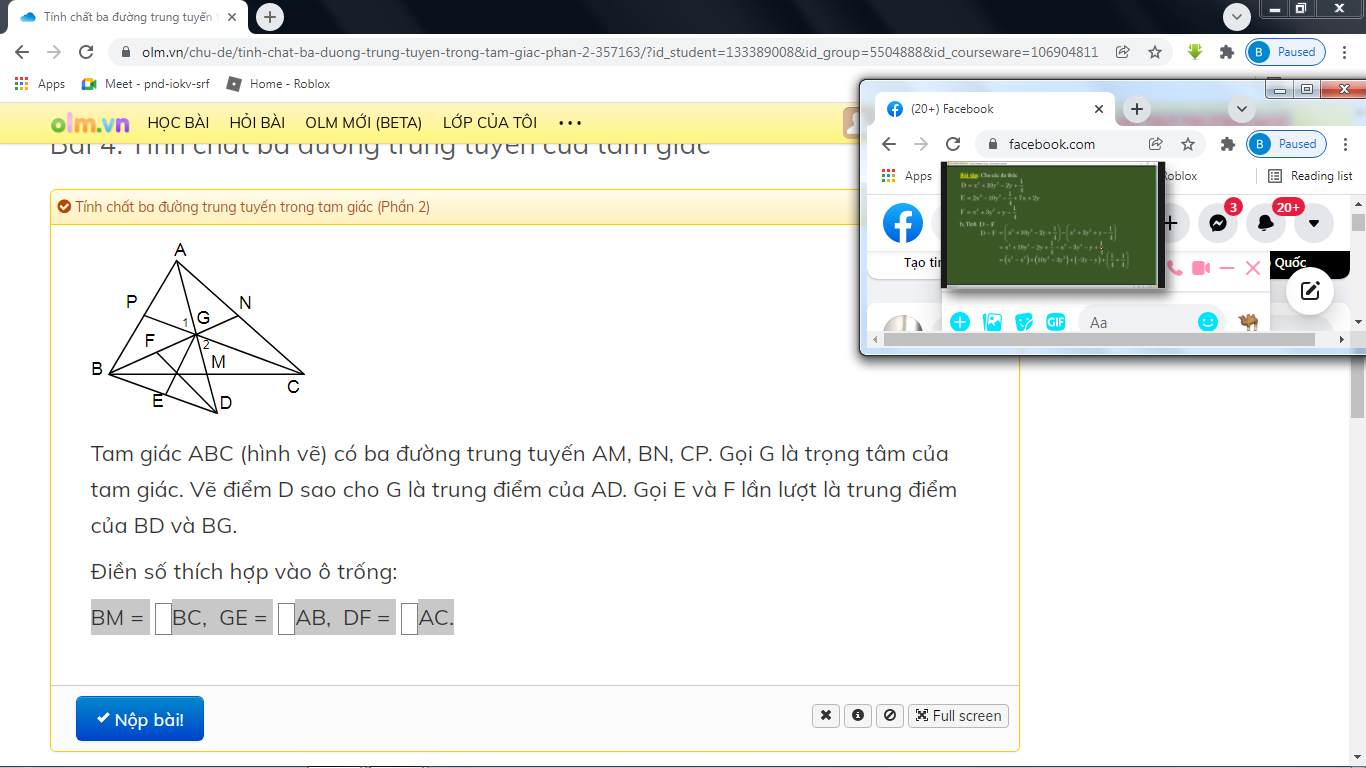
Tam giác ABC (hình vẽ) có ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác. Vẽ điểm D sao cho G là trung điểm của AD. Gọi E và F lần lượt là trung điểm của BD và BG.
Điền số thích hợp vào ô trống:
BM =....BC, GE =....AB, DF =....AC.
\(BM=\dfrac{1}{2}BC\)
\(GE=\dfrac{1}{2}AB\)
DF=AC
Đúng 0
Bình luận (0)
1)Cho tam giác ABC vuông tại A. gọi P,M,N lần lượt là trung điểm AB,BC,AC. cmr:\(AM^2+BN^2+CP^2=\dfrac{3}{2}BC^2\)
2)Cho tam giác ABC vuông tại A. gọi P,M,N lần lượt là trung điểm AB,BC,AC. cmr:
a)\(AB^2+BC^2+CA^2=\dfrac{4}{3}\left(AM^2+BN^2+CP^2\right)\)
b)nếu \(\widehat{A}=90^0\Leftrightarrow5AM^2=BN^2+CP^2\)
B1
Áp dụng định lý Pytago vào các tam giác vuông ta được:
PC^2=AP^2+AC^2
BN^2=AB^2+AN^2
BC^2=AB^2+AC^2
Theo tính chất tam giác vuông ta được:
AM=\(\dfrac{1}{2}\)BC=>AM^2=\(\dfrac{1}{4}\)BC^2
Từ trên =>AM^2+BN^2+CP^2=
\(\dfrac{1}{4}\)BC^2+AB^2+\(\dfrac{\left(AC\right)^2}{4}\)+AC^2+\(\dfrac{\left(AB\right)^2}{4}\)=\(\dfrac{2\left(BC\right)^2}{4}\)+BC^2=\(\dfrac{3}{2}\)BC^2(đpcm)
\(\dfrac{1}{4}\)
Đúng 0
Bình luận (0)
ẦN MINH HOÀNG2GP
Izumiki AkikoKien NguTrần Thân Đồng
QuNguTrần Việt Linh
yễn HoànHuỳnh Thoại
g Đình Bảo
Nguyễn Hoàng Đình Bảo
Phương HÀ
Thanh Hằng
ốc Lộc
yen
Đúng 0
Bình luận (2)
cho tam giác abc trên các cạnh bc ca ab lấy các điểm m,n,p sao cho bm/bc=cn/ca=ap/ab=k CHỨNG MINH am,bn,cp là 3 cạnh của 1 tam giác tìm già trị của k để diện tích tam giác tạo bới ba đoạn thẳng am,bn,cp nhỏ nhất. Giup mik vs
chào kênh du túp!
Cho tam giác ABC, M thuộc BC, N thuộc AC sao cho BM/MC=2/3 ; CN/NA=3/5 , AM cắt BN tại O.
a) Tính tỉ số AO/AM
b) Lấy điểm P trên AB sao cho PB/BA=2/7 . Chứng minh: AM, BN, CP đồng quy