Chứng minh nếu M là trung điểm của AB thì vecMA+vecMB=vec0

Những câu hỏi liên quan
B1: Cho tam giác ABC có trọng tâm G. Tìm tập hợp điểm M sao cho |vecto MA+vec MB+ vec MC| =3 đvdd
B2: Cho tam giác ABC:
a) Xác định điểm I sao cho vecto IA+ 2vecIB+ vecIC = vec0
b) Chứng minh với mọi M có vecMA + 2vecMB + vecMC =4vecMI
c) Tìm tập hợp điểm M thỏa mãn độ dài của tổng vecMA + 2vecMB + vecMC =4
MỌI NG CỐ GIÚP MÌNH NHÉ
Gọi A’, B’ lần lượt là ảnh của A, B qua phép dời hình F. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’.
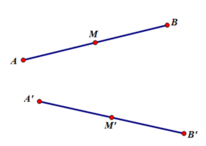
Gọi A', B', M' lần lượt là ảnh của A, B, M qua phép dời hình F
Theo tính chất 1 ⇒ AB = A'B' và AM = A'M' (1)
M là trung điểm AB ⇒ AM = 1/2 AB
Kết hợp (1) ⇒ A'M' = 1/2 A'B' ⇒ M' là trung điểm A'B'
Đúng 0
Bình luận (0)
Gọi A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’.
A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB
M’ = F(M) ⇒ A’M’ = kAM
M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’
Vậy M’ là trung điểm của A’B’
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB và trung điểm M của nó. Chứng minh rằng nếu C là điểm nằm giữa M và B thì CM =(CA-CB)/2
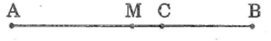
Vì M là trung điểm AB nên AM = MB
Vì M nằm giữa A và C nên AM + MC = AC
Vì C nằm giữa B và M nên BC + MC = BM ⇒ BC = BM – MC
Suy ra: AC > BC
Ta có: AC – BC = (AM + MC) – (BM – MC )
= AM + MC – BM + MC = 2MC
⇒ CM = (CA-CB)/2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, M là trung điểm của BC
a) Chứng minh rằng: AM = BC : 2;
b) Chứng minh rằng: Nếu C = 30 độ thì AB = BC : 2
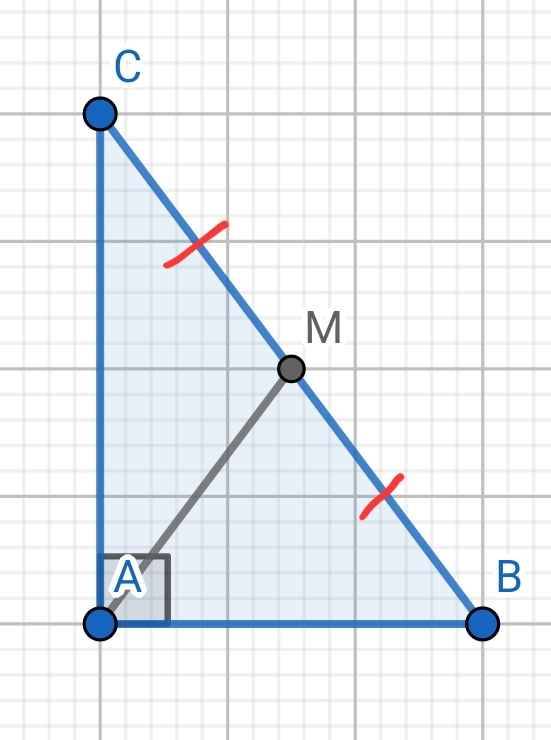
a) ∆ABC vuông tại A
M là trung điểm BC
⇒ AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
b) ∆ABC vuông tại A có ∠C = 30⁰
⇒ ∠B = 90⁰ - 30⁰ = 60⁰
Do AM = BM (cmt)
⇒ ∆ABM cân tại M
Lại có ∠ABM = ∠B = 60⁰
⇒ ∆ABM đều
⇒ AB = AM = BM = BC : 2
Đúng 1
Bình luận (0)
Trên đường thẳng xy lấy 2 điểm A và B.Gọi M là trung điểm của AB.O là 1 điểm bất kì trên đường thẳng xy.
a/ chứng minh nếu O thuộc AM thì OM=OA-OB/2.
b/ chứng minh nếu O không thuộc AB thì OM=OA + OB/2.
help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Trên đường thẳng xy lấy 2 điểm A và B.Gọi M là trung điểm của AB.O là 1 điểm bất kì trên đường thẳng xy.
a/ chứng minh nếu O thuộc AM thì OM=OA-OB/2.
b/ chứng minh nếu O không thuộc AB thì OM=OA + OB/2.
Đúng 0
Bình luận (0)
Cho ABC có E và F lần lượt là trung điểm của AB và AC.
a/ Chứng minh EF là đường trung bình của ABC.
b/Chứng minh BEFC là hình thang.
c/ Nếu AB=AC thì BEFC là hình gì ?
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔABC
Đúng 1
Bình luận (0)
giúp tớ mng ơi, nhanh nhé
Cho tam giác ABC vuông tại A, M là trung điểm của BC
a) Chứng minh rằng: AM = BC : 2;
b) Chứng minh rằng: Nếu C = 30 độ thì AB = BC : 2
a: Gọi D là điểm đối xứng của A qua M
Xét tứ giác ABDC có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AD
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AD=BC
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB có trung điểm là M
a) Chứng minh rằng nếu C điểm thuộc tia đối của tia BA thì CM=(CA+CB):2
b) Chứng minh rằng nếu C là điểm nằm giữa 2 điểm M và B thì CM=(CA-CB):2
_Giúp mình với ! Mình cần gấp ! Ngay mai mình phải nộp bài rồi!_













