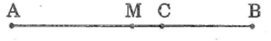
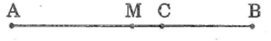
Vì M là trung điểm AB nên AM = MB
Vì M nằm giữa A và C nên AM + MC = AC
Vì C nằm giữa B và M nên BC + MC = BM ⇒ BC = BM – MC
Suy ra: AC > BC
Ta có: AC – BC = (AM + MC) – (BM – MC )
= AM + MC – BM + MC = 2MC
⇒ CM = (CA-CB)/2
Cho đoạn thẳng AB và trung điểm M của nó.
a. Chứng tỏ rằng nếu C là điểm thuộc tia đối của tia BA thì CM=CA+CB/2
b. Chứng tỏ rằng nếu C là điểm nằm giữa M và B thì CM=CA-CB/2
Cho đoạn thẳng AB và trung điểm M của nó:
a, Chứng tỏ rằng: Nếu C là điểm thuộc tia đối của tia BA thì CM=CA+CB/2
b, Chứng tỏ rằng: Nếu C là điểm nằm giữa M và B thì CM=CA-CB/2
Cho đoạn thẳng AB và trung điểm M của nó.
a. Chứng tỏ rằng nếu C là điểm thuộc tia đối của tia BA thì CM là (CA+CB):2
b. Chứng tỏ rằng nếu C là điểm nằm giữa M và B thì CM là (CA-CB):2
Cho đoạn thẳng AB và trung điểm M của nó.
a) Chứng tỏ rằng nếu C là điểm thuộc tia đối của tia BA thì CM=CA+CB:2
b) Chứng tỏ rằng nếu C là điểm nằm giữa M và B thì CM=CA-CB:2
cho đoạn thẳng AB và trung điểm M của nó
a. Chứng tỏ rằng nếu C là điểm thuộc tia đối của tia BA thì CM=CA+CB/2
b. Chứng tỏ rằng nếu C là điểm nằm giữa M và B thì CM=CA - CB/2
Cho đoạn thẳng AB và M là trung điểm của nó
a) Chứng tỏ rằng nếu C là đường thuộc tia BA thì CM = CA + CB /2
b) Chứng tỏ rằng nếu C là điểm nằm giữa M và B thì CM = CA - CB /2
Cho đoạn thẳng AB va trung điểm M của nó . Chứng tỏ rằng nếu C nằm giữa hai điểm M và B Thì CM = (CA-CB):2
Cho đoạn thẳng AB và trung điểm M của nó.
a) Biết AB = 10 cm. Tính MB
b) Chứng tỏ rằng:
1. Nếu C là điểm thuộc tia đối của tia BA thì CM = CA+CB:2
2. Nếu C là điểm nằm giữa M và B thì CM = CA-CB:2
Cho đoạn thẳng AB và trung điểm M của nó.
a, Chứng tỏ rằng nếu C là điểm nằm giữa M và B thi CM = (CA - CB):2
b, Chứng tỏ rằng nếu C là điểm thuộc tia đối của tia BA thì CM = (CA + BC):2
