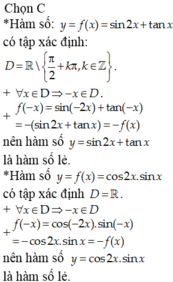Giải pt sau: cosx.cos2x=cos13x

Những câu hỏi liên quan
Giải các phương trình sau cosx.cos2x = 1 + sinx.sin2x
cosx.cos2x = 1 + sinx.sin2x
⇔ cosx.cos2x - sinx.sin2x = 1
⇔ cos3x = 1 ⇔ 3x = k2π
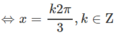
Đúng 0
Bình luận (0)
giải các pt
a) \(sin2x-2sinx=0\)
b) \(cosx.cos4x-cosx.cos2x=0\)
c) \(cos11x.cos3x=cos17x.cos9x\)
d) \(sin18x.cos13x=sin9x.cos4x\)
\(sin2x-2sinx=0\)
\(\Leftrightarrow2sinx.cosx-2sinx=0\)
\(\Leftrightarrow sinx\left(cosx-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=0\\cosx=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=k2\pi\end{matrix}\right.\) \(\Rightarrow x=k\pi\)
\(cosx.cos4x-cosx.cos2x=0\)
\(\Leftrightarrow cosx\left(cos4x-cos2x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\\cos4x=cos2x\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\4x=2x+k2\pi\\4x=-2x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=k\pi\\x=\frac{k\pi}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(cos11x.cos3x=cos17x.cos9x\)
\(\Leftrightarrow\frac{1}{2}\left(cos24x+cos8x\right)=\frac{1}{2}\left(cos26x+cos8x\right)\)
\(\Leftrightarrow cos24x=cos26x\)
\(\Rightarrow\left[{}\begin{matrix}26x=24x+k2\pi\\26x=-24x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{k\pi}{25}\end{matrix}\right.\)
\(sin18x.cos13x=sin9x.cos4x\)
\(\Leftrightarrow\frac{1}{2}\left(sin31x+sin5x\right)=\frac{1}{2}\left(sin13x+sin5x\right)\)
\(\Leftrightarrow sin31x=sin13x\)
\(\Rightarrow\left[{}\begin{matrix}31x=13x+k2\pi\\31x=\pi-13x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{k\pi}{9}\\x=\frac{\pi}{44}+\frac{k\pi}{22}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
giải phương trình
\(\dfrac{1-cosx.cos2x}{sin2x}-\dfrac{1}{cosx}=4sin^2x-sinx-1\)
giải chi tiết nha
Sin3x=Cosx.Cos2x (tan^2x+tan2x)
ĐKXĐ: cos2x<>0 và cosx<>0
=>x<>pi/2+kpi và x<>pi/4+kpi/2
PT\(\Leftrightarrow sin3x=cosx\cdot cos2x\cdot\left(\dfrac{sin^2x}{cos^2x}+\dfrac{sin2x}{cos2x}\right)\)
\(\Leftrightarrow sin3x\cdot cosx=sin^2x\cdot cos2x+sin2x\cdot cos^2x\)
\(\Leftrightarrow sinx\left(3-4sin^2x\right)\cdot cosx=sin^2x\cdot cos2x+sin2x\cdot cos^3x\)
=>sinx=0 hoặc \(\left(3-4sin^2x\right)cosx=sinx\cdot cos2x+2cos^3x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=kpi\\x=\dfrac{pi}{4}+kpi\left(loại\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tính giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{1-Cosx.Cos2x}{x^2}\)
Ko sử dụng L'Hopital:
\(\lim\limits_{x\rightarrow0}\dfrac{1-cosx+cosx\left(1-cos2x\right)}{x^2}=\lim\limits_{x\rightarrow0}\dfrac{2sin^2\dfrac{x}{2}+2cosx.sin^2x}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{1}{2}\left(\dfrac{sin\dfrac{x}{2}}{\dfrac{x}{2}}\right)^2+\lim\limits_{x\rightarrow0}2cosx\left(\dfrac{sinx}{x}\right)^2=\dfrac{1}{2}.1^2+2.1.1^2=\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
c/m : 1/cosx.cos2x + 1/cos2x.cos3x +... +1/cos7x.cos8x = (tan8x- tanx)/sinx
Giải các phương trình:
1, cosx - \(\sqrt{3}sinx=2cos\left(\frac{\pi}{3}-x\right)\)
2, sin5x +cos5x = \(\sqrt{2}cos13x\)
3, \(\left(3cosx-4sinx-6\right)^2+2=-3\left(3cosx-4sinx-6\right)\)
a/
\(\Leftrightarrow cosx.\frac{1}{2}-\frac{\sqrt{3}}{2}sinx=cos\left(\frac{\pi}{3}-x\right)\)
\(\Leftrightarrow cosx.cos\left(\frac{\pi}{3}\right)-sinx.sin\left(\frac{\pi}{3}\right)=cos\left(\frac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=cos\left(\frac{\pi}{3}-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{3}=\frac{\pi}{3}-x+k2\pi\\x+\frac{\pi}{3}=-\frac{\pi}{3}+x+k2\pi\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=k\pi\)
b/
\(\Leftrightarrow\sqrt{2}sin\left(5x+\frac{\pi}{4}\right)=\sqrt{2}cos13x\)
\(\Leftrightarrow cos\left(\frac{\pi}{4}-5x\right)=cos13x\)
\(\Leftrightarrow\left[{}\begin{matrix}13x=\frac{\pi}{4}-5x+k2\pi\\13x=-\frac{\pi}{4}+5x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{72}+\frac{k\pi}{9}\\x=-\frac{\pi}{32}+\frac{k\pi}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
Đặt \(3cosx-4sinx-6=t\)
Pt trở thành:
\(t^2+2=-3t\Leftrightarrow t^2+3t+2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3cosx-4sinx-6=-1\\3cosx-4sinx-6=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3cosx-4sinx=5\\3cosx-4sinx=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx.\frac{3}{5}-sinx.\frac{4}{5}=1\\cosx.\frac{3}{5}-sinx.\frac{4}{5}=\frac{4}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(x+a\right)=1\\cosx\left(x+a\right)=\frac{4}{5}\end{matrix}\right.\) (với góc \(a\in\left[0;\pi\right]\) sao cho \(cosa=\frac{3}{5}\))
\(\Leftrightarrow\left[{}\begin{matrix}x+a=k2\pi\\x+a=\pm\left(\frac{\pi}{2}-a\right)+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-a+k2\pi\\x=-a\pm\left(\frac{\pi}{2}-a\right)+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
giải pt sau để pt vô nghiệm
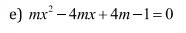
\(\text{∆}=\left(-4m\right)^2-4.m.\left(4m-1\right)\)
\(=16m^2-16m^2+4m\)
\(=4m\)
phương trình vô nghiệm khi \(\text{∆}< 0\)
\(\Rightarrow4m< 0\)
⇒ \(m< 0\)
Đúng 4
Bình luận (0)
`\Delta'=(-2m)^2-m(4m-1)=4m^2-4m^2+m=m`
Để phương trình vô nghiệm thì `\Delta'<0 => m<0`
Đúng 3
Bình luận (0)
nhận xét , đánh giá việc thực hành tiết kiệm của bản thân và những người xung quanh , phê phán những biểu hiện lãng phí
Đúng 1
Bình luận (0)
Cho các hàm số lượng giác
y
sin
2
x
+
tan
x
,
y
cos
2
x
.
sin
x
,
y
sin
x
+
2
,
y
cos
x
.
cos
2
x
. Số hàm số lẻ có được từ các hàm số trên là A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho các hàm số lượng giác y = sin 2 x + tan x , y = cos 2 x . sin x , y = sin x + 2 , y = cos x . cos 2 x . Số hàm số lẻ có được từ các hàm số trên là
A. 0
B. 1
C. 2
D. 3