Tam giác ABC vuông ở A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính góc B và góc C.

Những câu hỏi liên quan
1. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB= 25cm, HC= 64cm. Tính AH, AC, góc B và góc C
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=40cm\\AC=8\sqrt{89}cm\end{matrix}\right.\)
Xét ΔACH vuông tại H có
\(\sin\widehat{C}=\dfrac{AH}{AC}=\dfrac{5}{\sqrt{89}}\)
\(\Leftrightarrow\widehat{C}\simeq32^0\)
hay \(\widehat{B}=58^0\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính góc B , C
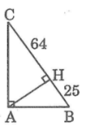
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
A H 2 = H B . H C
Suy ra:

Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A = 90 độ , đường cao AH
Biết BH = 25cm , HC = 64cm . Tính góc B , góc C
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\)
hay AH=40(cm)
Xét ΔABH vuông tại H có
\(\tan\widehat{B}=\dfrac{AH}{HB}=\dfrac{40}{25}=\dfrac{8}{5}\)
\(\Leftrightarrow\widehat{B}\simeq58^0\)
hay \(\widehat{C}=32^0\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A giải Tam giác ABC biết: a) Góc B 35 độ, BC40 cmb) AB70cm, AC60cmc) AB6cm, góc B60 độd) AB5cm, AC7cm 2) Cho tam giác ABC góc A 90 độ đường cao AH biết HB25cm, HC 64cm tín số đo góc B và C3)Tam giác ABC có góc A 90 độ, AB21cm, ggos C 40 độ tính độ dài đường phân giác BD4) Tam giác ABC có góc B70 độ góc C35 độ đường cao AH5cm tính độ dài AB,AC,B
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A giải Tam giác ABC biết: a) Góc B= 35 độ, BC=40 cm
b) AB=70cm, AC=60cm
c) AB=6cm, góc B=60 độ
d) AB=5cm, AC=7cm
2) Cho tam giác ABC góc A =90 độ đường cao AH biết HB=25cm, HC =64cm tín số đo góc B và C
3)Tam giác ABC có góc A =90 độ, AB=21cm, ggos C =40 độ tính độ dài đường phân giác BD
4) Tam giác ABC có góc B=70 độ góc C=35 độ đường cao AH=5cm tính độ dài AB,AC,B
Tam giác ABC vuông tại A ; đường cao AH; biết HB = 25cm; HC = 64 cm. Tính góc B
A. 42 °
B. 32 °
C. 58 o
D. 51 o
Đáp án C
Ta có: BC = HB + HC = 25 + 64 = 89 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
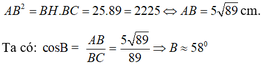
Đúng 0
Bình luận (0)
Cho tam giácABC vuông tại A, đường cao AH. Cho HB 25cm, HC 64cm. a) Tính chu vi và diện tích tam giác ABC b) Tính góc B, góc C ...
Đọc tiếp
Cho tam giácABC vuông tại A, đường cao AH. Cho HB = 25cm, HC = 64cm. a) Tính chu vi và diện tích tam giác ABC b) Tính góc B, góc C c) Kẻ HM vuông góc AB, HN vuông góc AC. Tính MN
a: BC=25+64=89cm
AH=căn 25*64=40cm
S ABC=1/2*40*89=1780cm2
AB=căn 25*89=5căn 89cm
AC=căn 64*89=8 căn 89
=>C=13căn 89+89(cm)
b: tan B=AC/AB=8/5
=>góc B=58 độ
=>góc C=32 độ
c:
góc AMH=góc ANH=góc MAN=90 độ nên AMHN là hcn
=>MN=AH=40cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, biết HB 9; HC 16. Tính góc B và góc C. A.
B
^
53
0
8
;
C
^
36
0
52
B.
B
^
36
0
52...
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH, biết HB = 9; HC = 16. Tính góc B và góc C.
A. B ^ = 53 0 8 ' ; C ^ = 36 0 52 '
B. B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
C. B ^ = 48 0 35 ' ; C ^ = 41 0 25 '
D. B ^ = 41 0 25 ' ; C ^ = 48 0 35 '
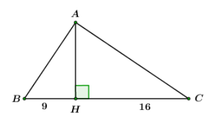
Ta có: BC = BH + CH = 9 + 16 = 25
Áp dụng hệ thức lượng cho ABC vuông tại A có đường cao AH ta có:
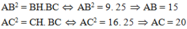
Xét ABC vuông tại A ta có:
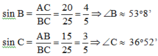
Đáp án cần chọn là: A
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao Ah .Biết HB = 25 cm, hc=64 cm .Tính góc B và góc C cua tam giác trên.
Bài 1.Tam giác ABC vuông tại A, có AB 21cm, widehat{C} 40°, phân giác BD của góc ABC, D ∈ AC. Tínha) độ dài đoạn thẳng AC, BCb) độ dài đoạn thẳng BDBài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 25cm, HC 64cm. Tính widehat{B}, widehat{C}Bài 3. Cho tam giác ABC vuông tại A có widehat{B} 30 °, AB 6cma) Giải tam giác vuông ABCb) Vẽ đường cao AH và trung tuyến Am của tam giác ABC. Tính diện tích tam giác AHM
Đọc tiếp
Bài 1.Tam giác ABC vuông tại A, có AB = 21cm, \(\widehat{C}\) = 40°, phân giác BD của góc ABC, D ∈ AC. Tính
a) độ dài đoạn thẳng AC, BC
b) độ dài đoạn thẳng BD
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính \(\widehat{B},\) \(\widehat{C}\)
Bài 3. Cho tam giác ABC vuông tại A có \(\widehat{B}\) = 30 °, AB = 6cm
a) Giải tam giác vuông ABC
b) Vẽ đường cao AH và trung tuyến Am của tam giác ABC. Tính diện tích tam giác AHM
Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)
Đúng 0
Bình luận (0)












