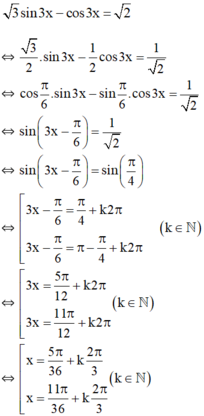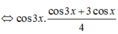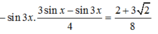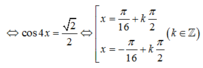sin3x-√3 cos3x=sinxcos2x-√3 sin2xcosx

Những câu hỏi liên quan
Giải các phương trình sau
a) \(sin^6x+cos^6x=cos2x+\dfrac{1}{16}\)
b) \(sin^4\dfrac{x}{2}+cos^4\dfrac{x}{2}=\dfrac{5}{2}-2sinx\)
c) \(cos5xcosx=cos4xcos2x+4-3sin^2x\)
d) \(2cosxcos2x=1+cos2x+cos3x\)
e) \(sin3x+cos2x=2\left(sin2xcosx-1\right)\)
a.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=cos2x+\dfrac{1}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x=cos2x+\dfrac{1}{16}\)
\(\Leftrightarrow\dfrac{15}{16}-\dfrac{3}{4}\left(1-cos^22x\right)=cos2x\)
\(\Leftrightarrow\dfrac{3}{4}cos^22x-cos2x+\dfrac{3}{16}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{4-\sqrt{7}}{6}\\cos2x=\dfrac{4+\sqrt{7}}{6}>1\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(\dfrac{4-\sqrt{7}}{6}\right)+k\pi\)
Đúng 1
Bình luận (0)
b.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{5}{2}-2sinx\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^2x=\dfrac{5}{2}-2sinx\)
\(\Leftrightarrow\dfrac{1}{2}sin^2x-2sinx+\dfrac{3}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=3\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
Đúng 0
Bình luận (0)
c.
\(\Leftrightarrow\dfrac{1}{2}cos6x+\dfrac{1}{2}cos4x=\dfrac{1}{2}cos6x+\dfrac{1}{2}cos2x+4-3\left(\dfrac{1}{2}-\dfrac{1}{2}cos2x\right)\)
\(\Leftrightarrow\dfrac{1}{2}\left(2cos^22x-1\right)=\dfrac{1}{2}cos2x+\dfrac{5}{2}+\dfrac{3}{2}cos2x\)
\(\Leftrightarrow cos^22x-2cos2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=3\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow2x=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Nghiệm của phương trình
sin
3
x
+
3
cos
3
x
–
3
sin
x
cos
2
x
–
sin
2
x
cos
x
0
là: A.
±
π
3
+
k
π
,
k
∈
ℤ
...
Đọc tiếp
Nghiệm của phương trình sin 3 x + 3 cos 3 x – 3 sin x cos 2 x – sin 2 x cos x = 0 là:
A. ± π 3 + k π , k ∈ ℤ h o ặ c π 4 + k π , k ∈ ℤ
B. π 3 + k π , k ∈ ℤ h o ặ c π 4 + k π , k ∈ ℤ
C. - π 3 + k π , k ∈ ℤ h o ặ c π 4 + k π , k ∈ ℤ
D. ± π 3 + k 2 π , k ∈ ℤ h o ặ c π 4 + k 2 π , k ∈ ℤ
Chọn A
Ta có: sin 3 x + 3 cos 3 x – 3 sin x cos 2 x – sin 2 x cos x = 0
Do cosx=0 không là nghiệm của phương trình nên chia hai vế cho cos 3 x ≠ 0 ta được phương trình:

Đúng 0
Bình luận (0)
•Sin3x - sin5x = sin2x
•Cosx + cos2x + cos3x = -1
•Sin2x + sin22x +sin23x + sin24x = 2
•1 + 2 sinxcos2x = sinx + cos2x
•Tan3x - tanx = sin2x
•(1-tanx)(1+sin2x) = 1+ tanx
\(\frac{ }{ }\)
Xem thêm câu trả lời
Giải phương trình √3 sin3x – cos3x = √2.
Câu 21:
sin3x -\(\sqrt{3}\) cos3x =2cos5x
sin3x(cosx - sin3x) + cos3x(sinx - cos3x)= 0
\(sin3x\left(cosx-sin3x\right)+cos3x\left(sinx-cos3x\right)=0\\ \Leftrightarrow sin3x\cdot cosx+cos3x\cdot sinx=sin^23x+cos^23x\\ \Leftrightarrow sin4x=1=sin\frac{\pi}{2}\\ \Leftrightarrow4x=\frac{\pi}{2}+k2\pi\\ \Leftrightarrow x=\frac{\pi}{8}+\frac{k\pi}{2}\)
Đúng 0
Bình luận (0)
chứng minh sin3x-cos3x=2(sinx+cosx)^3-3(sinx+cosx)
\(sin3x-cos3x=\left(3sinx-4sin^3x\right)-\left(4cos^3x-3cosx\right)\)
\(=3\left(sinx+cosx\right)-4\left(sin^3x+cos^3x\right)\)
\(=2\left(sin^3x+cos^3x\right)-6\left(sin^3x+cos^3x\right)+3\left(sinx+cosx\right)\)
\(=2\left(sin^3x+cos^3x\right)-6\left(sinx+cosx\right)\left(1-sinx.cosx\right)+3\left(sinx+cosx\right)\)
\(=2\left(sin^3x+cos^3x\right)-3\left(sinx+cosx\right)\left(1-2sinx.cosx\right)\)
\(=2\left(sin^3x+cos^3x\right)+6sinx.cosx\left(sinx+cosx\right)-3\left(sinx+cosx\right)\)
\(=2\left(sinx+cosx\right)^3-3\left(sinx+cosx\right)\) (đpcm)
Tìm các họ nghiệm của phương trình
cos
3
x
cos
3
x
-
sin
3
x
sin
3
x
2
+
3
2
8
Đọc tiếp
Tìm các họ nghiệm của phương trình cos 3 x cos 3 x - sin 3 x sin 3 x = 2 + 3 2 8
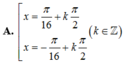
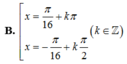
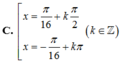
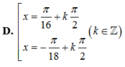
(sin3x+cosx)sin3x+(cos3x+sinx)cos3x/ cos4x = 1+tan2x/1-tan2x
\(\frac{\left(sin3x+cosx\right)sin3x+\left(cos3x+sinx\right)cos3x}{cos4x}\)
\(=\frac{sin^23x+sin3x.cosx+cos^23x+cos3x.sinx}{cos4x}=\frac{1+sin3x.cosx+cos3x.sinx}{cos4x}\)
\(=\frac{1+sin4x}{cos4x}=\frac{sin^22x+cos^22x+2sin2x.cos2x}{cos^22x-sin^22x}=\frac{\left(cos2x+sin2x\right)^2}{\left(cos2x-sin2x\right)\left(cos2x+sin2x\right)}\)
\(=\frac{cos2x+sin2x}{cos2x-sin2x}=\frac{1+\frac{sin2x}{cos2x}}{1-\frac{sin2x}{cos2x}}=\frac{1+tan2x}{1-tan2x}\)
Đúng 0
Bình luận (0)
Giải phương trình: \(sin3x-cos3x+sinx+cosx=\dfrac{1}{sin3x+cosx}-\dfrac{1}{cos3x-sinx}\)
ĐKXĐ: ...
\(sin3x-cos3x+sinx+cosx=\dfrac{sin3x-cos3x+sinx+cosx}{\left(sin3x+cosx\right)\left(cos3x-sinx\right)}\)
\(\Rightarrow\left[{}\begin{matrix}sin3x-cos3x+sinx+cosx=0\left(1\right)\\\left(sin3x+cosx\right)\left(cos3x-sinx\right)=1\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow3sinx-4sin^3x-4cos^3x+3cosx+sinx+cosx=0\)
\(\Leftrightarrow sinx+cosx+sin^3x+cos^3x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)\left(1-sinx.cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2-sinx.cosx\right)=0\)
\(\Leftrightarrow sinx+cosx=0\) (loại)
(2) \(\Leftrightarrow sin3x.cos3x-sinx.cosx-sin3x.sinx+cos3x.cosx=1\)
\(\Leftrightarrow\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x+cos4x=1\)
\(\Leftrightarrow\dfrac{1}{2}\left(3sin2x-4sin^32x\right)-\dfrac{1}{2}sin2x+1-2sin^22x=1\)
\(\Leftrightarrow sin2x-2sin^32x-2sin^22x=0\)
\(\Leftrightarrow-sin2x\left(2sin^22x+2sin2x-1\right)=0\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)