1, - Xét phương trình hoành độ giao điểm :\(2x^2=ax+b\)

\(\Rightarrow2x^2-ax-b=0\left(I\right)\)

Mà (P) tiếp xúc với d .

Nên PT ( I ) có duy nhất một nghiệm .

\(\Leftrightarrow\Delta=\left(-a\right)^2-4.2.\left(-b\right)=a^2+8b=0\)

Lại có : d đi qua A .

\(\Rightarrow b+0a=-2=b\)

\(\Rightarrow a=4\)

2. Tương tự a

3. - Xét phương trình hoành độ giao điểm :\(2x^2=2m+1\)

\(\Rightarrow2x^2-2m-1=0\)

Có : \(\Delta^,=\left(-m\right)^2-\left(-1\right).2=m^2+3\)

=> Giao điểm của P và d là : \(\left\{{}\begin{matrix}x_1=\dfrac{m+\sqrt{m^2+3}}{2}\\x_2=\dfrac{m-\sqrt{m^2+3}}{2}\end{matrix}\right.\)

Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d

2x² = x + 1 ⇔ 2x² – x – 1 = 0 ⇔ 2x² – 2x + x – 1 = 0

⇔ 2x(x – 1) + (x− 1) = 0

⇔ (2x + 1) (x – 1) = 0

⇔ x = − 1 2 x = 1

Vậy có hai giao điểm của đường thẳng d và parabol (P)

Đáp án cần chọn là: D

a: 

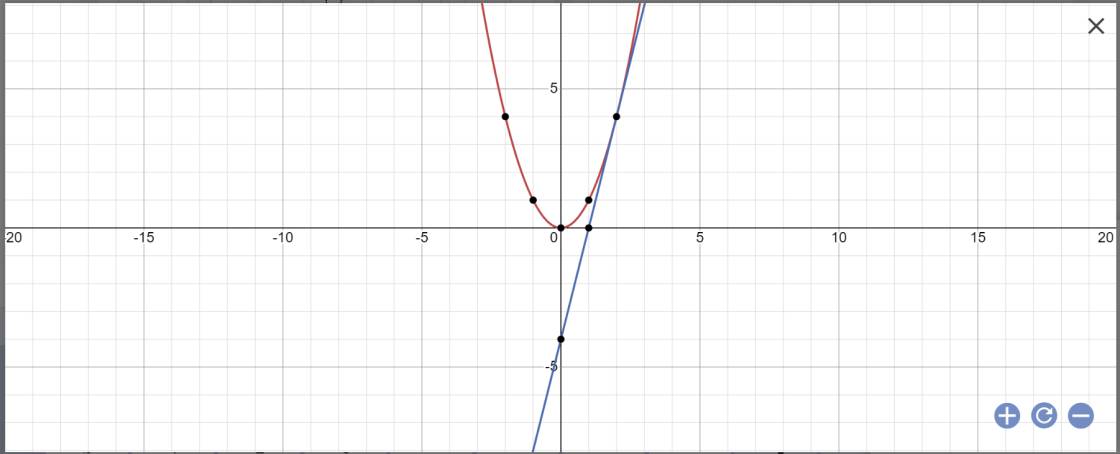
b: PTHĐGĐ là:

2x^2-(2m-2)x+m-1=0

Δ=(2m-2)^2-4*2*(m-1)

=4m^2-8m+4-8m+8

=4m^2-16m+12

=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)

Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0

=>m>3 hoặc m<1

làm bài này đâu nhất thiết phải dùng cách nào đâu bạn, vận dụng cách khoa học nhất là đc rồi nhé 

a, bạn tự vẽ 

b, Theo bài ra ta có hệ 

\(\left\{{}\begin{matrix}2x^2+4x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x^2+4x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+1\right)^2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)

Vậy (P) cắt (d) tại A(-1;2) 

a: PTHĐGĐ là:

x^2-3x+2=0

=>(x-2)(x-1)=0

=>x=2 hoặc x=1

Khi x=2 thì y=2^2=4

Khi x=1 thì y=1^2=1

b: Δ=(2m+2)^2-4(2m-3)

=4m^2+8m+4-8m+12

=4m^2+16>0

=>Phương trình luôn có hai nghiệm

a, Gọi ptđt (d) có dạng y = ax + b 

\(\left(d\right)//y=3x+1\Leftrightarrow\hept{\begin{cases}a=3\\b\ne1\end{cases}}\)

đt (d) đi qua A(3;7) <=> \(7=3a+b\)(*) 

Thay a = 3 vào (*) ta được : \(9+b=7\Leftrightarrow b=-2\)( tmđk )

Vậy ptđt có dạng y = 3x - 2

b, Hoành độ giao điểm thỏa mãn phương trình 

\(x^2=3x-2\Leftrightarrow x^2-3x+2=0\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\Leftrightarrow x=1;x=2\)

\(\Rightarrow y=1;y=4\)

Vậy (d) cắt (P) tại A( 1;1 ) ; B( 2 ; 4 )

a, Phương trình đường thẳng (d) là: y = ax + b 

Vì đường thẳng (d) song song với đường thẳng y = 3x + 1 nên

⇒⇒ {a=a′b≠b′{a=a′b≠b′ ⇔⇔ {a=3b≠1{a=3b≠1

Với a = 3 ta được pt đường thẳng (d): y = 3x + b

Vì đường thẳng (d) đi qua điểm A(3;7) nên thay x = 3; y = 7 ta được:

7 = 3.3 + b

⇔⇔ b = -2 (TM)

Vậy phương trình đường thẳng (d) là: y = 3x - 2

Chúc bn học tốt!

k mình nha

sao chép bài của Trương Huy Hoàng ở H đc đấy nhỉ Nguyễn Đặng Hưng

b. Phương trình hoành độ giao điểm:

\(x^2=4x-m\Leftrightarrow x^2-4x+m=0\) (1)

d cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm pb

\(\Leftrightarrow\Delta'=4-m>0\Rightarrow m< 4\)

Khi đó kết hợp hệ thức Viet và điều kiện đề bài:

\(\left\{{}\begin{matrix}x_1+x_2=4\\2x_1+x_2=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=4\\x_1=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-9\\x_2=13\end{matrix}\right.\)

Mà \(x_1x_2=m\)

\(\Rightarrow m=-9.13=-117\)

a) Thay m=6 vào (d), ta được: y=4x-6

Phương trình hoành độ giao điểm của (P) và (d) là:

\(2x^2=4x-6\)

\(\Leftrightarrow2x^2-4x+6=0\)

\(\text{Δ}=\left(-4\right)^2-4\cdot2\cdot6=16-48=-32\)(loại)

Vì Δ<0 nên phương trình vô nghiệm

Vậy: Khi m=6 thì (P) và (d) không có điểm chung

1) ĐK \(\hept{\begin{cases}x\ne y\\y\ge-1\end{cases}}\)

Đặt \(\hept{\begin{cases}\frac{1}{x-y}=a\left(a\ne0\right)\\\sqrt{y+1}=b\left(b\ge0\right)\end{cases}}\)hệ phương trình đã cho trở thành

\(\hept{\begin{cases}2a+b=4\\a-3b=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+b=4\\2a-6b=-10\end{cases}}\Leftrightarrow\hept{\begin{cases}7b=14\\2a+b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=2\end{cases}\left(tm\right)}\)

\(\Rightarrow\hept{\begin{cases}\frac{1}{x-y}=1\\\sqrt{y+1}=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=1\\y+1=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=4\\y=3\end{cases}}\left(tm\right)\)

Vậy ... 

ĐKXĐ: x ≠ y ; y ≥ − 1 Đặt 1 x − y = a ; √ y + 1 = b (ĐK: a ≠ 0 ; b ≥ 0 ) Khi đó hệ phương trình trở thành { 2 a + b = 4 a − 3 b = − 5 ⇔ { 6 a + 3 b = 12 a − 3 b = − 5 ⇔ { 7 a = 7 b = 4 − 2 a ⇔ { a = 1 ( tm ) b = 2 ( tm ) Với ⎧ ⎪ ⎨ ⎪ ⎩ a = 1 b = 2 ⇒ ⎧ ⎪ ⎨ ⎪ ⎩ 1 x − y = 1 √ y + 1 = 2 ⇒ { x − y = 1 y + 1 = 4 ⇔ { x − 3 = 1 y = 3 ⇔ { x = 4 ( tm ) y = 3 ( tm ) Vậy hệ phương trình đã cho có nghiệm { x = 4 y = 3 . 2) Xét phương trình hoành độ giao điểm giữa đường thẳng ( d ) và Parabol ( P ) là: x 2 = 2 ( m − 1 ) x − m 2 + 2 m ⇔ x 2 − 2 ( m − 1 ) x + m 2 − 2 m = 0 (1) a) Với m = 2 phương trình (1) trở thành: x 2 − 2 ( 2 − 1 ) x + 2 2 − 2.2 = 0 ⇔ x 2 − 2 x = 0 ⇔ x ( x − 2 ) = 0 ⇔ [ x = 0 x = 2 - Với x = 0 ⇒ y = 0 2 = 0 ⇒ A ( 0 ; 0 ) - Với x = 2 ⇒ y = 2 2 = 4 ⇒ B ( 2 ; 4 ) Vậy khi m = 2 thì ( P ) cắt ( d ) tại hai điểm phân biệt A ( 0 ; 0 ) ; B ( 2 ; 4 ) . b) Ta có: Δ ′ = b ′ 2 − a c = [ − ( m − 1 ) ] 2 − ( m 2 − 2 m ) = m 2 − 2 m + 1 − m 2 + 2 m = 1 > 0 Do Δ ′ > 0 nên phương trình (1) luôn có hai nghiệm phân biệt x 1 ; x 2 với mọi m . ⇒ Đường thẳng ( d ) luôn cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ x 1 ; x 2 với mọi m . Khi đó theo hệ thức Viet, ta có: { x 1 + x 2 = 2 m − 2 x 1 x 2 = m 2 − 2 m Để đường thẳng ( d ) cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ đối nhau ⇔ x 1 + x 2 = 0 ⇔ 2 m − 2 = 0 ⇔ m = 1 ( tm ) Vậy m = 1 thì đường thẳng ( d ) luôn cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ đối nhau.

ĐKXĐ: x ≠ y ; y ≥ − 1 Đặt 1 x − y = a ; √ y + 1 = b (ĐK: a ≠ 0 ; b ≥ 0 ) Khi đó hệ phương trình trở thành { 2 a + b = 4 a − 3 b = − 5 ⇔ { 6 a + 3 b = 12 a − 3 b = − 5 ⇔ { 7 a = 7 b = 4 − 2 a ⇔ { a = 1 ( tm ) b = 2 ( tm ) Với ⎧ ⎪ ⎨ ⎪ ⎩ a = 1 b = 2 ⇒ ⎧ ⎪ ⎨ ⎪ ⎩ 1 x − y = 1 √ y + 1 = 2 ⇒ { x − y = 1 y + 1 = 4 ⇔ { x − 3 = 1 y = 3 ⇔ { x = 4 ( tm ) y = 3 ( tm ) Vậy hệ phương trình đã cho có nghiệm { x = 4 y = 3 . 2) Xét phương trình hoành độ giao điểm giữa đường thẳng ( d ) và Parabol ( P ) là: x 2 = 2 ( m − 1 ) x − m 2 + 2 m ⇔ x 2 − 2 ( m − 1 ) x + m 2 − 2 m = 0 (1) a) Với m = 2 phương trình (1) trở thành: x 2 − 2 ( 2 − 1 ) x + 2 2 − 2.2 = 0 ⇔ x 2 − 2 x = 0 ⇔ x ( x − 2 ) = 0 ⇔ [ x = 0 x = 2 - Với x = 0 ⇒ y = 0 2 = 0 ⇒ A ( 0 ; 0 ) - Với x = 2 ⇒ y = 2 2 = 4 ⇒ B ( 2 ; 4 ) Vậy khi m = 2 thì ( P ) cắt ( d ) tại hai điểm phân biệt A ( 0 ; 0 ) ; B ( 2 ; 4 ) . b) Ta có: Δ ′ = b ′ 2 − a c = [ − ( m − 1 ) ] 2 − ( m 2 − 2 m ) = m 2 − 2 m + 1 − m 2 + 2 m = 1 > 0 Do Δ ′ > 0 nên phương trình (1) luôn có hai nghiệm phân biệt x 1 ; x 2 với mọi m . ⇒ Đường thẳng ( d ) luôn cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ x 1 ; x 2 với mọi m . Khi đó theo hệ thức Viet, ta có: { x 1 + x 2 = 2 m − 2 x 1 x 2 = m 2 − 2 m Để đường thẳng ( d ) cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ đối nhau ⇔ x 1 + x 2 = 0 ⇔ 2 m − 2 = 0 ⇔ m = 1 ( tm ) Vậy m = 1 thì đường thẳng ( d ) luôn cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ đối nhau.

1) ĐK \(\hept{\begin{cases}x\ge0\\y\ne1\end{cases}}\)

Đặt \(\hept{\begin{cases}2\sqrt{x}=a\left(a\ge0\right)\\\frac{1}{y-1}=b\left(b\ne0\right)\end{cases}}\)hệ phương trình đã cho trở thành 

\(\hept{\begin{cases}a+3b=5\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+6b=10\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}7b=7\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=1\end{cases}\left(tm\right)}\)

\(\Rightarrow\hept{\begin{cases}2\sqrt{x}=2\\\frac{1}{y-1}=1\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\left(tm\right)\)

Vậy ... 

1,\(\left\{{}\begin{matrix}2\sqrt{x}+\dfrac{3}{y-1}=5\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\)       ĐKXĐ:x≥o,y≠1

⇔\(\left\{{}\begin{matrix}4\sqrt{x}+\dfrac{6}{y-1}=10\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y-1}=7\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y-1=1\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-1=1\\4\sqrt{x}-\dfrac{1}{1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\4\sqrt{x}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\\sqrt{x}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\left(TM\right)\)

vậy hpt đã cho có nghiệm duy nhất (x,y)=(1,2)

2,a, xét pthđgđ của (d) và (p) khi m=3:

x\(^2\)=3x-1⇔\(x^2-3x+1=0\)

Δ=(-3)\(^2\)-4.1.1=5>0

⇒pt có 2 nghiệm pb

\(x_1=\dfrac{3+\sqrt{5}}{2}\) ,\(x_2=\dfrac{3-\sqrt{5}}{2}\)

thay x=x\(_1\)=\(\dfrac{3+\sqrt{5}}{2}\) vào hs y=x\(^2\) ta được:

y=(\(\dfrac{3+\sqrt{5}}{2}\))\(^2\)=\(\dfrac{14+6\sqrt{5}}{4}\)⇒A(\(\dfrac{3+\sqrt{5}}{2},\dfrac{14+6\sqrt{5}}{4}\))

thay x=x\(_2\)=\(\dfrac{3-\sqrt{5}}{2}\) vào hs y=x\(^2\) ta được:

y=\(\left(\dfrac{3-\sqrt{5}}{2}\right)^2=\dfrac{14-6\sqrt{5}}{4}\)⇒B(\(\dfrac{3-\sqrt{5}}{2},\dfrac{14-6\sqrt{5}}{4}\))

vậy tọa độ gđ của (d) và (p) là A(\(\dfrac{3+\sqrt{5}}{2},\dfrac{14+6\sqrt{5}}{4}\)) và B (\(\dfrac{3-\sqrt{5}}{2},\dfrac{14-6\sqrt{5}}{4}\))

b,xét pthđgđ của (d) và (p) :

\(x^2=mx-1\)⇔\(x^2-mx+1=0\) (*)

                       Δ=(-m)\(^2\)-4.1.1=m\(^2\)-4

⇒pt có hai nghiệm pb⇔Δ>0

                                  ⇔m\(^2\)-4>0⇔m>16

với m>16 thì pt (*) luôn có hai nghiệm pb \(x_1,x_2\)

theo hệ thức Vi-ét ta có:

(I) \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=1\end{matrix}\right.\)

\(x_1,x_2\) TM \(x_2\)(x\(_1\)\(^2\)+1)=3

⇒\(x_2.x_1^2\)+\(x_2\)=3⇔\(x_2.x_1.x_1+x_2=3\)⇔(\(x_2.x_1\))(\(x_1+x_2\))=3 (**)

thay  (I) vào (**) ta được:

1.m=3⇔m=3 (TM m≠0)

vậy m=3 thì (d) cắt (p) tại hai điểm pb có hoanh độ \(x_1.x_2\) TM \(x_2\)(\(x_1^2+1\))=3

                      

 

 

♬