cho hình vuông abcd trên ab lấy điểm m tia dm cắt ab tại f và ac ở e giả sử ed bằng 15 và em bằng 9 tính mf

Những câu hỏi liên quan
Cho hình vuông abcd. Gọi m là một điểm trên cạnh bc. Kẻ đường thẳng dm cắt ac ở e, ab ở f. Biết de = 15, em = 9. Tính mf
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
c) Biết ∠BAD = 60o, AB = a. Tính diện tích hình thoi ABCD theo a.
c) ΔABD cân (AB = AD (gt)) có ∠BAD = 60o nên ΔABD đều
kẻ BJ ⊥ AD ta có:
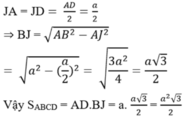
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A, M là điểm nằm trên cạnh BC (M khác B, C). Vẽ M, E lần lượt vuông góc với AB, AC tại E và F. Trên tia MF lấy I sao cho MI ABa) Tứ giác ABMI; AEMF là hình gì? Vì sao?b) Giả sử BC 8cm. Tính diện tích tam giác ABC.c) Gọi D là điểm đối xứng với A qua BC. Chứng minh AB CD và BF I DEd) Chứng minh các đường thẳng DM, BF, CE đồng quy Mình cần gấp câu c, d ạ
Đọc tiếp
Cho tam giác ABC vuông cân tại A, M là điểm nằm trên cạnh BC (M khác B, C). Vẽ M, E lần lượt vuông góc với AB, AC tại E và F. Trên tia MF lấy I sao cho MI = AB
a) Tứ giác ABMI; AEMF là hình gì? Vì sao?
b) Giả sử BC= 8cm. Tính diện tích tam giác ABC.
c) Gọi D là điểm đối xứng với A qua BC. Chứng minh AB = CD và BF I DE
d) Chứng minh các đường thẳng DM, BF, CE đồng quy Mình cần gấp câu c, d ạ
a: Xét tứ giác ABMI có
MI//AB
MI=AB
Do đó; ABMI là hình bình hành
Xét tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hìnhchữ nhật
b: \(AB=\sqrt{\dfrac{BC^2}{2}}=\sqrt{32}=4\sqrt{2}\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot4\sqrt{2}\cdot4\sqrt{2}=2\sqrt{2}\cdot4\sqrt{2}=16\left(cm^2\right)\)
c: A đối xứng D qua BC
nên CA=CD
=>CD=AB
Đúng 0
Bình luận (0)
Bài 1: Cho hình bình hành ABCD có BD = 8cm, O là giao điểm của hai đường chéo. E, M thuộc cạnh CD sao cho: DE = EM = MC, AE cắt BD tại K, OM cắt AB tại F. CMR:
a) AF = 1/3 AB
b) Tính DK
Bài 2: Cho hình bình hành ABCD. Trên tia đối của tia BC lấy điểm E sao cho BE = BC. Trên tia đối của tia BC lấy điểm F sao cho CD = CF. CMR: các đoạn thẳng AC, ED và BF đồng quy.
cho hình ABCD là hình thoi, góc B bằng 60 độ, trên tia đối của tia AB lấy điểm E sao cho ED cắt BC tại F, M là giao điểm của EC và AF. chứng minh góc ACE bằng góc CFA
Cho tam giác ABC cân tại A ( góc A nhọn ), trên hai cạnh AB và AC lần lượt lấy hai điểm E và D sao cho AE AD. Trên tia đối của tia CA lấy điểm F sao cho CF CD a , Chứng minh : ED // BC b , Chứng minh : Đường thẳng vuông góc với đoạn AB tại B, đường thẳng vuông góc với AC tại C và đường trung trực của đoạn thẳng EF cùng đi qua một điểm. c, Giả sử góc A bằng 20 độ, trên AB lấy điểm K sao cho AK BC. Tính góc BCK
Đọc tiếp
Cho tam giác ABC cân tại A ( góc A nhọn ), trên hai cạnh AB và AC lần lượt lấy hai điểm E và D sao cho AE = AD. Trên tia đối của tia CA lấy điểm F sao cho CF = CD
a , Chứng minh : ED // BC
b , Chứng minh : Đường thẳng vuông góc với đoạn AB tại B, đường thẳng vuông góc với AC tại C và đường trung trực của đoạn thẳng EF cùng đi qua một điểm.
c, Giả sử góc A bằng 20 độ, trên AB lấy điểm K sao cho AK = BC. Tính góc BCK
Cho tam giác ABC cân tại A ( góc A nhọn ), trên hai cạnh AB và AC lần lượt lấy hai điểm E và D sao cho AE AD. Trên tia đối của tia CA lấy điểm F sao cho CF CD a , Chứng minh : ED // BC b , Chứng minh : Đường thẳng vuông góc với đoạn AB tại B, đường thẳng vuông góc với AC tại C và đường trung trực của đoạn thẳng EF cùng đi qua một điểm. c, Giả sử góc A bằng 20 độ, trên AB lấy điểm K sao cho AK BC. Tính góc BCK
Đọc tiếp
Cho tam giác ABC cân tại A ( góc A nhọn ), trên hai cạnh AB và AC lần lượt lấy hai điểm E và D sao cho AE = AD. Trên tia đối của tia CA lấy điểm F sao cho CF = CD
a , Chứng minh : ED // BC
b , Chứng minh : Đường thẳng vuông góc với đoạn AB tại B, đường thẳng vuông góc với AC tại C và đường trung trực của đoạn thẳng EF cùng đi qua một điểm.
c, Giả sử góc A bằng 20 độ, trên AB lấy điểm K sao cho AK = BC. Tính góc BCK
hey,mk có quen bạn ko?
vì trong danh sách bạn cũng có người có tên giống hệt cậu lun
Đúng 0
Bình luận (0)
cho tam giác cân ABC, AB = AC. Trên cạnh BC lấy điểm D. Trên tia đối của tia BC lấy điểm E sao cho BD = BE. Các đường vuông góc với BC kẻ từ D và E cắt AB và AC lần lượt ở M và N. Chứng minh DM = ED
cho tam giac ABC vuông tại A có AM và BN là hai đường trung tuyến cắt nhau tại G . biết AB=21cm , AC=28cm . a)tính AG b) trên tia đối NB lấy E sao nho NB=NE.c/m EC=AB và EC//AB c)trên tia đối MA lấy F sao cho MA=MF . c/m 3 điểm E,C,F thẳng hàng
Cho mình xin phép trình bài theo kiểu lớp 8 ạ!
a) Xét ∆ABC vuông tại A có
BC=CA2+AB2(theo định lí pythagore)
<=>\(BC=\sqrt{AC^2+AB^2}\)
\(\Rightarrow BC=\sqrt{28^2+21^2}\)
\(\Rightarrow BC=35\)
Do AM là trung tuyến với cạnh BC
nên AM=BC:2
\(\Rightarrow AM=\dfrac{35}{2}\)
Mà G là trọng tâm của ∆ABC nên \(AG=\dfrac{2}{3}AM\Leftrightarrow AG=\dfrac{35}{3}\)
Đúng 0
Bình luận (0)

















