c) ΔABD cân (AB = AD (gt)) có ∠BAD = 60o nên ΔABD đều
kẻ BJ ⊥ AD ta có:
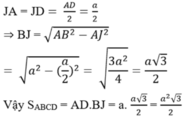
c) ΔABD cân (AB = AD (gt)) có ∠BAD = 60o nên ΔABD đều
kẻ BJ ⊥ AD ta có:
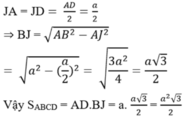
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
a) Chứng minh ID = 2IF.
cho hình thoi ABCD có hai đường chéo cắt nhau tại o trên tia đối của tia BA lấy BE=BA.Nối ED cắt AC ở I và BC tại F. a,Chứng minh ID =2IF
b,Nối EO cắt BC ở G, đường thẳng Ò cắt EC tại H. Chứng minh ba điểm A, G, H thẳng hàng
c, Biết góc BAD=60o , AB=a.Tính diện tích hình thoi ABCD theo a
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
b) Nối EO cắt BC ở G, đường thẳng OF cắt EC ở H. Chứng minh ba điểm A, G, H thẳng hàng.
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O .Trên tia đối của tia BA lấy điểm E sao cho BE=BA. Nối ED cắt AC ở I và BC ở F
a, Chứng minh ID=2IF
b, Nối EO cắt BC ở G , đường thẳng OF cắt EC ở H .Chứng minh ba điểm A,G,H thẳng hành
c, Biết tam giác =60 độ ,AB =a .Tính diện tích hình thoi ABCD theo a
Cho hình thoi ABCD, có 2 đường chéo cắt nhau tại O. Trên tia đối của tia BA, lấy BE=BA. Nối E,D cắt AC ở I và BC ở F
a) Cm: ID=2IF
b) Nối EO cắt BC ở G, đường thẳng OF cắt EC ở H. Cm 3 điểm A,G,H thẳng hàng.
c) Biết góc BAD = 60 độ. AB = a . TÍnh diện thích hình thoi ABCD theo a
Giúp mình vs!
Hình thoi ABCD,hai đường chéo cắt O .Trên tia đối tian BA lấy BE=BA,nối ED cắt AC ở I và BC ở F
a) chứng minh ID=2IF
b)nối EO cắt BC ở G,đường thẳng OF cắt EC ở H . chứng minh A,G,H thẳng hàng
c) Biết góc BAD = 60 độ , AB=a .Tính diện tích hình thoi ABCD theo a
Hình thoi ABCD,hai đường chéo cắt O .Trên tia đối tian BA lấy BE=BA,nối ED cắt AC ở I và BC ở F
a) chứng minh ID=2IF
b)nối EO cắt BC ở G,đường thẳng OF cắt EC ở H . chứng minh A,G,H thẳng hàng
c) Biết góc BAD = 60 độ , AB=a .Tính diện tích hình thoi ABCD theo a
cho hình thoi ABCD có 2 đường chéo cắt ở O .trên tia đối của AB lấy E sao cho AB=BE.NỐI ED cắt AC Ở I vÀ cắt BC ở F.
CM: ID=2IF
nối EO cắt BC ở G ,OF cắt CE ở H.CM:A, G, H THẲNG HÀNG
Bài 1: Cho hình bình hành ABCD có BD = 8cm, O là giao điểm của hai đường chéo. E, M thuộc cạnh CD sao cho: DE = EM = MC, AE cắt BD tại K, OM cắt AB tại F. CMR:
a) AF = 1/3 AB
b) Tính DK
Bài 2: Cho hình bình hành ABCD. Trên tia đối của tia BC lấy điểm E sao cho BE = BC. Trên tia đối của tia BC lấy điểm F sao cho CD = CF. CMR: các đoạn thẳng AC, ED và BF đồng quy.