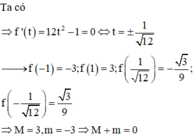Tìm giá trị nhỏ nhất m của biểu thức \(P=sin^2x+2cos^2x\)
Những câu hỏi liên quan
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức sau:
A=\(3\sin^2x+6cos^2x\)
Tìm giá trị nhỏ nhất của biểu thức:
\(M=\left(1+tg^2x\right)\left(1-sin^2x\right)+\left(1+cotg^2x\right)\left(1-cos^2x\right)-sinx.cosx\) \(\left(0^o< x< 90^o\right)\)
13 tháng 9 2016 lúc 18:14
tìm giá trị lớn nhất và giá trị nhỏ nhất của các biểu thức sau :
a) \(\sin^2x+\sin x\cos x+3\cos^2x\)
b) \(A\sin^2x+B\sin x\cos x+C\cos^2x\) (A , B , C là các hằng số )
1 tháng 10 2016 lúc 11:56
tìm giá trị lớn nhất và giá trị nhỏ nất của mỗi biểu thức sau :
a) \(\sin^2x+\sin x\cos x+3\cos^2x\)
b) \(A\sin^2x+B\sin x\cos x+C\cos^2x\) (A , B ,C là các hằng số)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) y=f(x)=\(\dfrac{4}{\sqrt{5-2cos^2xsin^2x}}\)
b)y=f(x)=\(3sin^2x+5cos^2x-4cos2x-2\)
c)y=f(x)=\(sin^6x+cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos x 1 + 2 cos 2 x . Tìm M + m
A. 3
B. 0
C. 1
D. 2
1 tháng 7 2020 lúc 22:00
Tìm giá trị lớn M và nhỏ nhất m của biểu thưc:
a) \(P=sin^2x+2cos^2x\)
b) \(P=8sin^2x+3cos2x\)
c) \(P=sin^4x-cos^4x\)
d) \(P=sin^6x+cos^6x\)
a/ \(P=sin^2x+cos^2x+cos^2x=1+cos^2x\)
Mà \(0\le cos^2x\le1\Rightarrow1\le P\le2\)
\(P_{min}=1\) khi \(cosx=0\)
\(P_{max}=2\) khi \(cosx=\pm1\)
b/ \(P=8sin^2x+3\left(1-2sin^2x\right)=3+2sin^2x\)
Mà \(0\le sin^2x\le1\Rightarrow3\le P\le5\)
\(P_{min}=3\) khi \(sinx=0\)
\(P_{max}=5\) khi \(sinx=\pm1\)
c/ \(P=\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)=sin^2x-cos^2x=-cos2x\)
Mà \(-1\le cos2x\le1\Rightarrow-1\le P\le1\)
\(P_{min}=-1\) khi \(cos2x=1\)
\(P_{max}=1\) khi \(cos2x=-1\)
d/ \(P=\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\)
\(=1-3sin^2x.cos^2x=1-\frac{3}{4}\left(2sinx.cosx\right)^2=1-\frac{3}{4}sin^22x\)
Mà \(0\le sin^22x\le1\Rightarrow\frac{1}{4}\le P\le1\)
\(P_{min}=\frac{1}{4}\) khi \(sin2x=\pm1\)
\(P_{max}=1\) khi \(sin2x=0\)
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức
M = 2x + | 2x - 5 |
Tìm giá trị nhỏ nhất của biểu thức:
\(M=x^4-2x^3+2x^2-2x+1\)
\(M=x^4-x^3-x^3+x^2+x^2-2x+1\)
\(=x^3\left(x-1\right)-x^2\left(x-1\right)+\left(x-1\right)^2\)
\(=\left(x-1\right)\left(x^3-x^2\right)+\left(x-1\right)^2\)
\(=\left(x-1\right)^2\cdot x^2+\left(x-1\right)^2=\left(x-1\right)^2\left(x^2+1\right)\)
\(\left(x-1\right)^2\ge0\)\(\forall x\)
\(x^2+1\ge1\)\(\forall x\)
Do đó: \(M>=1\)
Dấu = xảy ra khi x=0
Đúng 1
Bình luận (0)