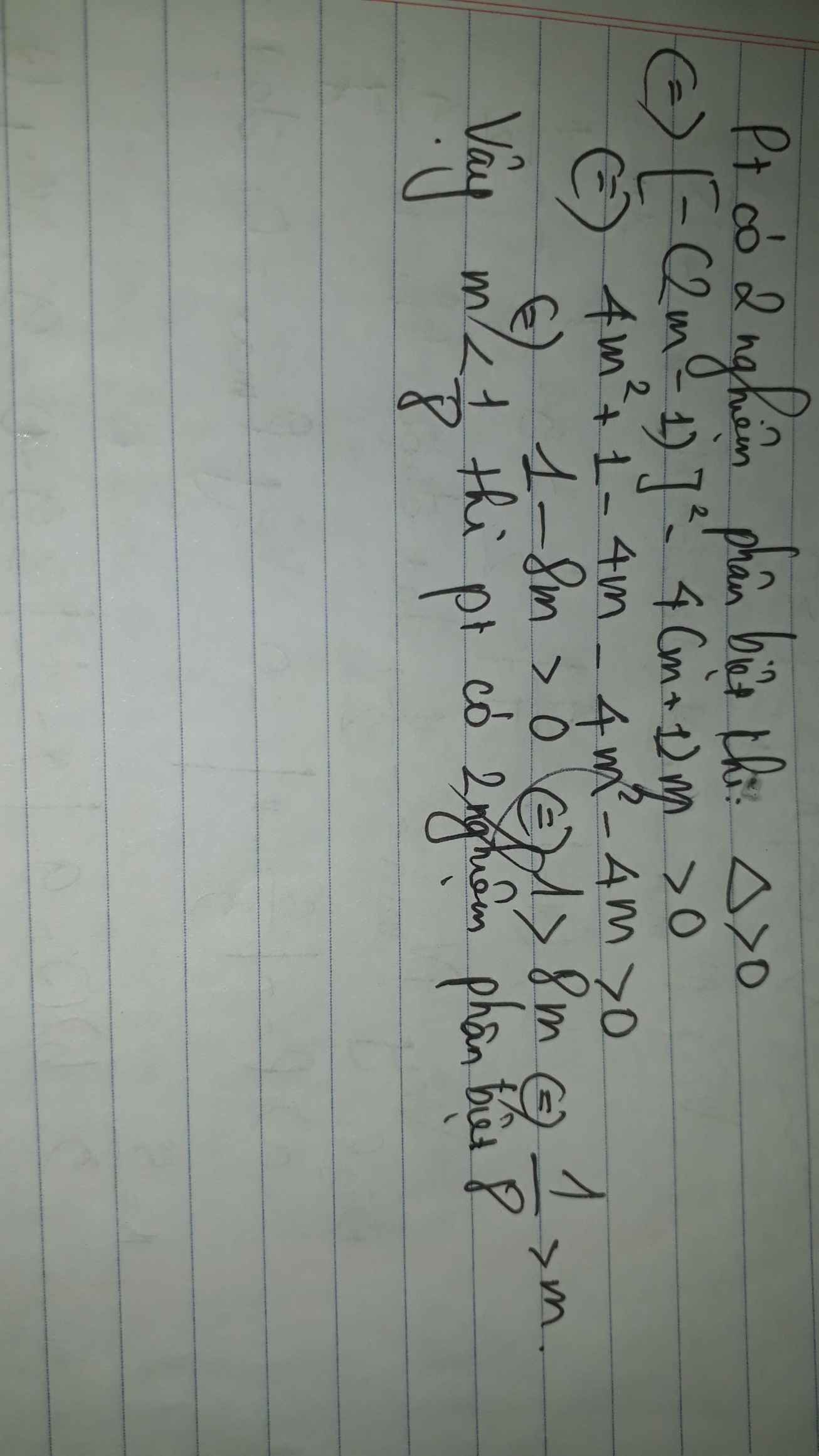a: \(\text{Δ}=\left(-4\right)^2-4\cdot2\cdot5\left(m-1\right)\)

\(=16-40\left(m-1\right)\)

\(=16-40m+40\)

=-40m+56

Để phương trình có hai nghiệm phân biệt nhỏ hơn 3 thì

\(\left\{{}\begin{matrix}-40m+56>0\\\dfrac{4}{2}< 6\end{matrix}\right.\Leftrightarrow-40m>-56\)

hay m<7/5

b: Để phương trình có hai nghiệm phân biệt lớn hơn 3 thì

\(\left\{{}\begin{matrix}-40m+56>0\\\dfrac{4}{2}>6\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

\(\text{Δ}=\left(-8\right)^2-4\cdot\left(-3\right)\cdot\left(m-1\right)\)

\(=64+12\left(m-1\right)\)

=64+12m-12

=12m+52

a: Để phương trình có hai nghiệm phân biệt nhỏ hơn 7 thì 

\(\left\{{}\begin{matrix}12m+52>0\\8< 14\end{matrix}\right.\Leftrightarrow m>-\dfrac{13}{4}\)

b: Để phương trình có hai nghiệm phân biệt lớn hơn 7 thì \(\left\{{}\begin{matrix}12m+52>0\\8>14\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

\(\left\{{}\begin{matrix}x^2+2xy-3y^2=-4\left(1\right)\\2x^2+xy+4y^2=5\left(2\right)\end{matrix}\right.\)\(với\)\(y=0\Rightarrow hpt\Leftrightarrow\left\{{}\begin{matrix}x^2=-4\\2x^2=5\end{matrix}\right.\)\(\left(loại\right)\)

\(y\ne0\) \(đặt:x=t.y\Rightarrow hpt\Leftrightarrow\left\{{}\begin{matrix}t^2y^2+2ty^2-3y^2=-4\left(3\right)\\2t^2y^2+ty^2+4y^2=5\left(4\right)\end{matrix}\right.\)

\(\Leftrightarrow5t^2y^2+10ty^2-15y^2=-8t^2y^2-4ty^2-16y^2\)

\(\Leftrightarrow13t^2y^2+14ty^2+y^2=0\)

\(\Leftrightarrow13t^2+14t+1=0\Leftrightarrow\left[{}\begin{matrix}t=-\dfrac{1}{13}\\t=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{13}y\left(5\right)\\x=-y\left(6\right)\end{matrix}\right.\)

\(thay\left(5\right)và\left(6\right)\) \(lên\left(1\right)hoặc\left(2\right)\Rightarrow\left(x;y\right)=\left\{\left(1;-1\right);\left(-1;1\right);\left(-\dfrac{1}{\sqrt{133}};\dfrac{13}{\sqrt{133}}\right)\right\}\)

\(pt:x^4-4x^3+x^2+6x+m+2=0\)

\(\Leftrightarrow x^4-4x^3+4x^2-3x^2+6x+m+2=0\)

\(\Leftrightarrow\left(x^2-2x\right)^2-3\left(x^2-2x\right)+m+2=0\left(1\right)\)

\(đặt:x^2-2x=t\ge-1\)

\(\Rightarrow\left(1\right)\Leftrightarrow t^2-3t=-m-2\)

\(xét:f\left(t\right)=t^2-3t\) \(trên[-1;+\text{∞})\) \(và:y=-m-2\)

\(\Rightarrow f\left(-1\right)=4\)

\(f\left(-\dfrac{b}{2a}\right)=-\dfrac{9}{4}\)

\(\left(1\right)\) \(có\) \(3\) \(ngo\) \(pb\Leftrightarrow-m-2=4\Leftrightarrow m=-6\)

\(\Delta=\left(2m-1\right)^2-4\cdot\left(m+1\right)\cdot m\)

\(=4m^2-4m+4-4m^2-4m\)

\(=-8m+4\)

Để phương trình có hai nghiệm phân biệt thì 

\(\left\{{}\begin{matrix}m+1\ne0\\-8m+4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\-8m>-4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)

Ta có: \(\text{Δ}=\left(1-4m\right)^2-4\left(3-2m\right)\left(1-2m\right)\)

\(=16m^2-8m+4-4\left(2m-3\right)\left(2m-1\right)\)

\(=16m^2-8m+4-4\left(4m^2-2m-6m+3\right)\)

\(=16m^2-8m+4-4\left(4m^2-8m+3\right)\)

\(=16m^2-8m+4-16m^2+32m-12\)

\(=24m-8\)

Để phương trình có hai nghiệm phân biệt thì

\(\left\{{}\begin{matrix}3-2m\ne0\\24m-8>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m\ne3\\24m>8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{3}{2}\\m>\dfrac{1}{3}\end{matrix}\right.\)

\(\Delta=\left[-2\left(m-1\right)\right]^2-4.\left(-2\right)\)

   \(=4m^2-8m+8+8\)

   \(=4m^2-8m+16\)

   \(=3m^2+\left(m-4\right)^2\)

Để pt có 2 nghiệm phân biệt thì \(\Delta>0\)

                                                  \(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>4\end{matrix}\right.\) \(\rightarrow m>4\)

Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\left(1\right)\\x_1x_2=-2\end{matrix}\right.\)

\(A=x_1^2+4x_2^2\)

\(A=x_1^2+\left(2x_2\right)^2\)

\(\Rightarrow Min_A=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x_1=0\\x_2=0\end{matrix}\right.\)

Thế vào (1) ta được: \(0=2m-2\)

                                \(\Leftrightarrow m=1\)

tui ko biết !!!!!

\(x^3-2mx^2+m^2x+x-m=0\Leftrightarrow x\left(x^2-2mx+m^2\right)+\left(x-m\right)=0\)

\(\Leftrightarrow x\left(x-m\right)^2+\left(x-m\right)=0\Leftrightarrow\left(x-m\right)\left(x^2-mx+1\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x-m=0\left(1\right)\\x^2-mx+1=0\left(2\right)\end{cases}}\)

Phương trình ba đầu có ba nghiệm phân biệt khi và chỉ khi phương trình 2 có hai nghiệm phân việt khác m

\(\Leftrightarrow\hept{\begin{cases}\Delta>0\\m^2-m^2+1\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}m^2-4>0\\1\ne0\end{cases}\Leftrightarrow}\orbr{\begin{cases}m>2\\m< -2\end{cases}}}\)

ĐỀ BÀi \(\Leftrightarrow x^3-2mx^2+m^2x+x-m=0\Leftrightarrow x\left(x^2-2mx+m^2\right)+x-m=0\)

\(\Leftrightarrow x\left(x-m\right)^2+\left(x-m\right)=0\Leftrightarrow\left(x-m\right)\left(x^2-mx+1\right)=0\Leftrightarrow\orbr{\begin{cases}x=m\\x^2-mx+1=0\left(#\right)\end{cases}}\)

để pt đã cho có 3 nghiệm phân biệt thì (#) có 2 nghiệm phân biệt khác m

dễ thấy x=m ko là nghiệm của (#) . Zậy (#)  có 2 nghiệm phân biệt khi

\(\Delta=m^2-4>0=>\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)

zậy,,,

\(\Leftrightarrow\left[\left(x-2\right)^2-4\right]^2-3\left(x-2\right)^2+m=0\)

\(\left(x-2\right)^2=t\ge0\Rightarrow pt\Leftrightarrow\left(t-4\right)^2-3t+m=0\)

\(\Leftrightarrow t^2-11t+16+m=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=11^2-4\left(16+m\right)>0\\x_1+x_2=11>0\left(tm\right)\\x_1x_2=16+m>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{57}{4}\\m< 16\end{matrix}\right.\Leftrightarrow m< \dfrac{57}{4}\)