Cho ΔABC có ba góc nhọn, kẻ AH ⊥BC(H∈BC) có BH<HC. Chứng minh AB<AC bằng hai cách khác nhau

Những câu hỏi liên quan
Cho tam giác ABC có ba góc nhọn, kẻ AH vuông góc với BC (H thuộc BC) có BH < HC. Chứng minh: AB < AC bằng hai cách khác nhau
Xét ΔABC có BH<HC
mà AB là đường xiên của BH
và AC là đường xiên của CH
nên AB<AC
Đúng 0
Bình luận (0)
Cho ΔABC có góc B nhọn và ABC = 2ACB. Kẻ AH ⊥ BC và kẻ tia phân giác BD của ABC. Trên tia đối của tia BA lấy điểm E sao cho BE = BH. Gọi I là giao điểm của EH và AC. Chứng minh rằng:
a) ACB = ABD và ABC = 2BEH
b) BD // EI
Cho ΔABC vuông tại A, AB = 5cm, BC = 13cm, kẻ AH vuông góc với BC tại H. Tính độ dài các đoạn AC, AH, BH, CH.
Xem chi tiết
- Áp dụng định lý pi ta go vào tam giác ABC vuông tại A ta được :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2+5^2=13^2\)
\(\Rightarrow AC=12\left(cm\right)\)
- Xét tam giác BHA và tam giác BAC có : \(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^o\\\widehat{B}\left(chung\right)\end{matrix}\right.\)
=> Hai tam giác trên đồng dạng .
=> \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
=> \(BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\)
=> \(CH=BC-BH=\dfrac{144}{13}\left(cm\right)\)
- Áp dụng định lý pi ta go vào tam giác ABH vuông tại H ta được :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH=\dfrac{60}{13}\left(cm\right)\)
Vậy ...
Đúng 1
Bình luận (1)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=13^2-5^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot13=5\cdot12\)
\(\Leftrightarrow AH\cdot13=60\)
hay \(AH=\dfrac{60}{13}cm\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2=5^2-\left(\dfrac{60}{13}\right)^2=\dfrac{625}{169}\)
hay \(BH=\dfrac{25}{13}cm\)
Ta có: BH+CH=BC(H nằm giữa B và C)
\(\Leftrightarrow CH=BC-BH=13-\dfrac{25}{13}\)
hay \(CH=\dfrac{144}{13}cm\)
Vậy: AC=12cm; \(AH=\dfrac{60}{13}cm\); \(BH=\dfrac{25}{13}cm\); \(CH=\dfrac{144}{13}cm\)
Đúng 1
Bình luận (1)
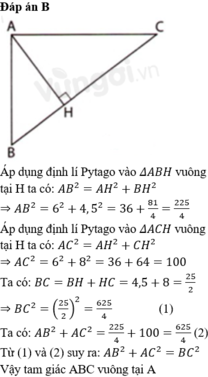
Cho tam giác ABC có
B
^
,
C
^
là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH6cm, BH4,5cm, HC8cm. Khi đó
Δ
A
B
C
là tam giác gì? A. Tam giác cân B. Tam giác vuông C. Tam giác vuông cân D. Tam giác đều
Đọc tiếp
Cho tam giác ABC có B ^ , C ^ là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH=6cm, BH=4,5cm, HC=8cm. Khi đó Δ A B C là tam giác gì?
A. Tam giác cân
B. Tam giác vuông
C. Tam giác vuông cân
D. Tam giác đều
* Cho ΔABC vuông tại A, biết AC= 12cm, BC=15cm
a. Giải tam giác ABC
b. Tính độ dài đường cao AH, đường phân giác AD của ΔABC
* Cho ΔABC có 3 góc nhọn, kẻ đường cao AH.
a. CM: sinA+cos A>1
b. CM: BC=AH. (cotgB+cotgC)
c. Biết AH=6cm, góc B=\(60^0\), góc C=\(45^0\). Tính diện tích ΔABC
Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)
Đúng 0
Bình luận (0)
. Cho ∆ABC nhọn, kẻ AH vuông góc với BC (H ∈BC). Cho biết AC = 20 cm, AH = 12cm, BH = 5cm. Tính độ dài cạnh AB, BC.
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=\sqrt{AC^2-AH^2}=16cm\)
Theo định lí Ptago tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+HB^2}=13cm\)
-> BC = HB + HC = 5 + 16 = 21 cm
Đúng 0
Bình luận (1)
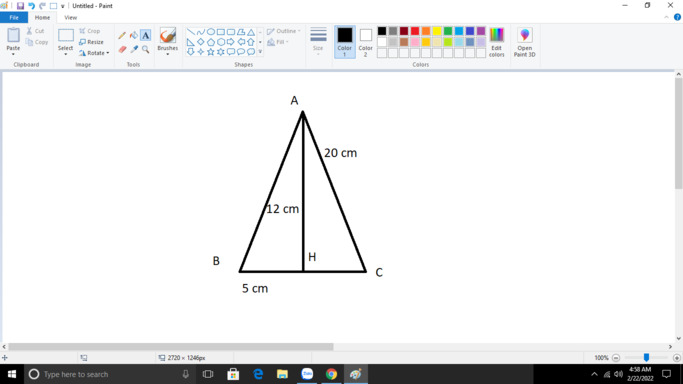
\(\text{Xét }\Delta AHB\text{ vuông tại }H\left(AH\perp BC\right)\text{có:}\)
\(AB^2=AH^2+BH^2\text{(định lí Py ta go)}\)
\(\Rightarrow AB^2=12^2+5^2=144+25=169\)
\(\Rightarrow AB=\sqrt{169}=13\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ vuông tại }H\left(AH\perp BC\right)\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC^2=AC^2-AH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow HC^2=20^2-12^2=400-144=256\)
\(\Rightarrow HC=\sqrt{256}=16\left(cm\right)\)
\(\Rightarrow BC=BH+HC\)
\(\Rightarrow BC=5+16=21\left(cm\right)\)
Đúng 2
Bình luận (0)
ΔABC có ∠B và ∠C nhọn. Gọi D là điểm bất kì thuộc cạnh BC, gọi H và K là chân các đường vuông góc kẻ từ B và C đến đường thẳng AD.
a, So sánh độ dài BH và BD; có khi nào BH=BD không?
b, So sánh tổng BH+CK với BC?
a: ΔBHD vuông tại H
=>BH<BD
BH=BD khi H trùng với D
=>AD vuông góc BC
b: ΔCKD vuông tại K
=>CK<CD
mà BH<BD
nên BH+CK<BC
Đúng 0
Bình luận (0)
cho tam giác nhọn abc ,kẻ ah vuông góc với bc( h thuộc bc) .cho ah=12cm bh=5cm và bc=14cm.Tính các độ dài ab và ac
Dựa theo định lý pytago:
=> BH2+AH2=AB2
=> AB2=52+122
AB2=25+144=169
=> AB=\(\sqrt{169}=13\left(cm\right)\)
Ta có: HC= BC-BH=14-5=9(cm)
Dựa theo định lý pytago:
AH2+HC2=AC2
=> AC2=122+92
AC2=144+81= 225(cm)
=> AC= \(\sqrt{225}=15\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác nhọn ABC, kẻ AH vuông góc với BC (H thuộc BC) cho biết AH=12 cm ,BH=5cm và BC =14cm tính độ dài AB và AC
a) Xét t/giác ABH vuông tại H , ta có: AB2 = AH2 + BH2 (Pi - ta - go)
=> AB2 = 122 + 52 = 169 => AB = 13 (cm)
Ta có: HC + BH = BC => HC = BC - BH = 14 - 5 = 9 (cm)
Xét t/giác AHC vuông tại H, có: AC2 = HC2 + AH2 (Pi - ta - go)
=> AC2 = 92 + 122 = 225 => AC = 15 (cm)
Đúng 1
Bình luận (0)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=12^2+5^2=169\)
hay AB=13(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=14-5=9(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+9^2=225\)
hay AC=15(cm)
Vậy: AB=13cm; AC=15cm
Đúng 0
Bình luận (0)
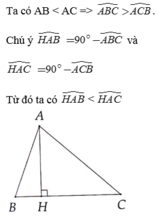
Cho tam giác ABC có ba góc nhọn, AB AC. Kẻ AH vuông góc với BC tại H. So sánh
H
A
B
^
và
H
A
C
^
.
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ AH vuông góc với BC tại H. So sánh và .

CÂU TRẢ LỜI CHÍNH XÁC NÈ