Theo định lí Pytago tam giác AHC vuông tại H
\(HC=\sqrt{AC^2-AH^2}=16cm\)
Theo định lí Ptago tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+HB^2}=13cm\)
-> BC = HB + HC = 5 + 16 = 21 cm
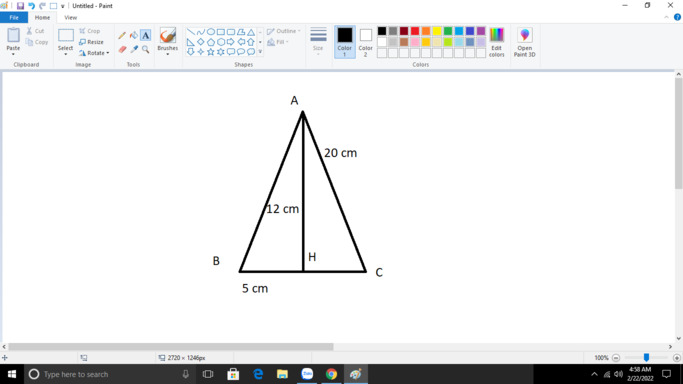
\(\text{Xét }\Delta AHB\text{ vuông tại }H\left(AH\perp BC\right)\text{có:}\)
\(AB^2=AH^2+BH^2\text{(định lí Py ta go)}\)
\(\Rightarrow AB^2=12^2+5^2=144+25=169\)
\(\Rightarrow AB=\sqrt{169}=13\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ vuông tại }H\left(AH\perp BC\right)\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC^2=AC^2-AH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow HC^2=20^2-12^2=400-144=256\)
\(\Rightarrow HC=\sqrt{256}=16\left(cm\right)\)
\(\Rightarrow BC=BH+HC\)
\(\Rightarrow BC=5+16=21\left(cm\right)\)













