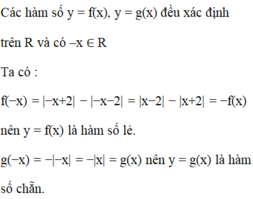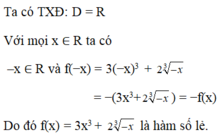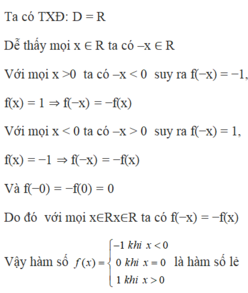Xét tính chẵn lẻ F(x)= tan²x + 6

Những câu hỏi liên quan
Xét tính chẵn lẻ của các hàm số lượng giác sau:
a) y = f(x) = sin3( 3x + 5π ) + cot( 2x - 7π )
b) y = f(x) = cot( 4x + 5π ).tan( 2x - 3π )
Xét tính chẵn - lẻ của hàm số:
a) \(y=x.cosx\)
b) \(y=5sin^2x+1\)
c) \(y=sinx.cosx\)
d) \(y=tanx+cotx\)
e) \(y=\dfrac{sinx-tanx}{sinx}\)
f) \(y=tan\left|x\right|\)
a: TXĐ: D=R
Với mọi x thuộc D thì -x cũng thuộc D
\(f\left(-x\right)=-x\cdot cos\left(-x\right)=-x\cdot cosx=-f\left(x\right)\)
=>f(x) lẻ
b: TXĐ: D=R
Với mọi x thuộc D thì -x cũng thuộc D
\(f\left(-x\right)=5\cdot sin^2\left(-x\right)+1=5\cdot sin^2x+1=f\left(x\right)\)
=>f(x) chẵn
c: TXĐ: D=R
Với mọi x thuộc D thì -x cũng thuộc D
\(f\left(-x\right)=sin\left(-x\right)\cdot cos\left(-x\right)=-sinx\cdot cosx=-f\left(x\right)\)
=>f(x) lẻ
Đúng 1
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau:
a) f (x) = -2x3+3x
b) f (x) = x2 + x
c) f (x) =\(\sqrt{6-3x}-\sqrt{6+3x}\)
d) f (x)= \(\dfrac{\sqrt{x+5}-\sqrt{5-x}}{4-x^2}\)
Mn giúp e bài này với ạ.E đang cần gấp ạ.
a: \(f\left(-x\right)=-2\cdot\left(-x\right)^3+3\cdot\left(-x\right)\)
\(=2x^3-3x\)
\(=-\left(-2x^3+3x\right)\)
=-f(x)
Vậy: f(x) là hàm số lẻ
c: TXĐ: D=[-2;2]
Nếu \(x\in D\Leftrightarrow-x\in D\)
\(f\left(-x\right)=\sqrt{6-3\cdot\left(-x\right)}-\sqrt{6+3\cdot\left(-x\right)}\)
\(=\sqrt{6+3x}-\sqrt{6-3x}\)
\(=-f\left(x\right)\)
Vậy: f(x) là hàm số lẻ
Đúng 3
Bình luận (2)
Xét tính chẵn, lẻ của hai hàm số:
f
(
x
)
x
+
2
-
x
-
2
,
g
(
x
)
-
x
A. f(x) là hàm số chẵn, g(x)là hàm số chẵn. B. f(x) là hàm số lẻ,g(x) là hàm số chẵn. C. f(x) là hàm số lẻ, g(x) là hàm số lẻ. D. f(x) là hàm s...
Đọc tiếp
Xét tính chẵn, lẻ của hai hàm số: f ( x ) = x + 2 - x - 2 , g ( x ) = - x
A. f(x) là hàm số chẵn, g(x)là hàm số chẵn.
B. f(x) là hàm số lẻ,g(x) là hàm số chẵn.
C. f(x) là hàm số lẻ, g(x) là hàm số lẻ.
D. f(x) là hàm số chẵn, g(x) là hàm số lẻ.
Đáp án B
+ Hàm số f(x) và g(x) đều có tập xác định là D= R.
+ Xét hàm số y=f(x) : Với mọi ![]() và
và
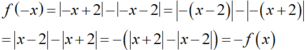
Nên y= f(x) là hàm số lẻ.
+ Xét hàm số y = g(x) :
Với mọi ![]() nên y = g(x) là hàm số chẵn.
nên y = g(x) là hàm số chẵn.
Chọn B.
Đúng 0
Bình luận (0)
Xét tính chẵn, lẻ của hai hàm số f(x) = |x + 2| − |x − 2|, g(x) = −|x|
A. f(x) là hàm số chẵn, g(x) là hàm số chẵn
B. f(x)là hàm số lẻ, g(x) là hàm số chẵn
C. f(x)là hàm số lẻ, g(x) là hàm số lẻ.
D. f(x)là hàm số chẵn, g(x) là hàm số lẻ
Xét tính chẵn, lẻ của hàm số f ( x ) = 3 x 3 + 2 x 3
A. hàm số lẻ
B. hàm số chẵn
C. không xét được tính chẵn lẻ
D. hàm số không chẵn, không lẻ
Xét tính chẵn, lẻ của hai hàm số
f
(
x
)
-
x
và
g
(
x
)
x
+
1
-
x
-
1
. A. f(x) là hàm số chẵn, g(x) là hàm số chẵn B. f(x)là hàm số lẻ, g(x) là hàm số chẵn C. f(x) là hàm số lẻ, g(x) là hàm số lẻ D. f(x) là hàm số chẵn, g(...
Đọc tiếp
Xét tính chẵn, lẻ của hai hàm số f ( x ) = - x và g ( x ) = x + 1 - x - 1 .
A. f(x) là hàm số chẵn, g(x) là hàm số chẵn
B. f(x)là hàm số lẻ, g(x) là hàm số chẵn
C. f(x) là hàm số lẻ, g(x) là hàm số lẻ
D. f(x) là hàm số chẵn, g(x) là hàm số lẻ
Tập xác định của hàm số f(x)và g(x) đều là ℝ .
Với x ∈ ℝ thì - x ∈ ℝ và ta có: f - x = - - x = - x = f x ;
g - x = - x + 1 - - x - 1 = x - 1 - x + 1 = - g x .
Vậy f(x)là hàm số chẵn, g(x) là hàm số lẻ. Đáp án là D.
Đúng 0
Bình luận (0)
Xét tính chẵn, lẻ của các hàm số:
a) \(y = \sin x\cos x\)
b) \(y = \tan x + \cot x\)
c) \(y = {\sin ^2}x\)
a) Ta có:
\(\left. \begin{array}{l}f\left( { - x} \right) = \sin \left( { - x} \right).\cos \left( { - x} \right) = - \sin x.\cos x\\f\left( x \right) = \sin x.\cos x\end{array} \right\} \Rightarrow f\left( { - x} \right) = - f\left( x \right)\)
Hàm số \(y = \sin x\cos x\) là hàm số lẻ
b) Ta có:
\(\left. \begin{array}{l}f\left( { - x} \right) = \tan \left( { - x} \right) + \cot \left( { - x} \right) = - \tan x - \cot x\\f\left( x \right) = \tan x + \cot x\end{array} \right\} \Rightarrow f\left( { - x} \right) = - f\left( x \right)\)
Hàm số \(y = \tan x + \cot x\) là hàm số lẻ
c) Ta có:
\(\left. \begin{array}{l}f\left( { - x} \right) = {\sin ^2}\left( { - x} \right) = {\left( { - \sin \left( x \right)} \right)^2} = {\sin ^2}x\\f\left( x \right) = {\sin ^2}x\end{array} \right\} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Hàm số \(y = {\sin ^2}x\) là hàm số chẵn
Đúng 0
Bình luận (0)
Xét tính chẵn lẻ của hàm số
f
(
x
)
−
1
k
h
i
x
0
0
k
h...
Đọc tiếp
Xét tính chẵn lẻ của hàm số f ( x ) = − 1 k h i x < 0 0 k h i x = 0 1 k h i x > 0
A. hàm số lẻ
B. hàm số chẵn
C. không xét được tính chẵn lẻ
D. hàm số không chẵn, không lẻ