Tổng bốn góc của 1 tứ giác bằng  360 °  nên: ∠A +  ∠ B +  ∠ C + ∠ D = 360 °

Suy ra:  ∠ A +  ∠ B =  360 °  – ( ∠ C + ∠ D) hay

∠ A +  ∠ B =  360 ° - 60 ° + 80 ° = 220 °  

Mà  ∠ A -  ∠ B = 10 °

Vậy  ∠ A = 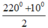 = 115 ° ,  ∠ B =  115 °  -  10 °  =  105 °

Ta có :

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

\(\Rightarrow\widehat{A}+\widehat{B}=360^o-\left(\widehat{C}+\widehat{D}\right)\)

\(\Rightarrow\widehat{A}+\widehat{B}=360^o-\left(60+80\right)=220^o\)

mà \(\widehat{A}-\widehat{B}=10^o\)

\(\Rightarrow\widehat{A}=\left(220-10\right):2=105^o\)

\(\Rightarrow\widehat{B}=105-10=95^o\)

Vậy \(\left\{{}\begin{matrix}\widehat{A}=105^o\\\widehat{B}=95^o\end{matrix}\right.\)

Tứ giác ABCD có: ( ko bik ghi góc nên ko ghi nha )

A + B + C + D = 360⁰ ( Tổng 4 góc của tứ giác )

A + B = 360⁰ - ( C + D )

A + B = 360⁰ - ( 60⁰ + 80⁰ )

A + B = 220⁰

A = [ ( A + B ) + ( A - B ) ] : 2 = ( 220⁰ + 10⁰ ) : 2 = 115⁰

A - B = 10⁰

→ B = A - 10⁰ = 115⁰ -10⁰ = 105^0.

\(a,=>\angle\left(B\right)+\angle\left(C\right)=100+80=180^o\)

mà 2 góc ở vị trí trong cùng phía \(=>AB//CD\)

=>ABCD là hình thang

b,\(\dfrac{\angle\left(A\right)}{\angle\left(D\right)}=\dfrac{6}{4}=>\angle\left(A\right)=\dfrac{6\angle\left(D\right)}{4}\)

\(=>\angle\left(A\right)+\angle\left(D\right)=180^o\)(góc trong cùng phía)

\(=>\dfrac{6\angle\left(D\right)}{4}+\angle\left(D\right)=180^o=>\angle\left(D\right)=72^o=>\angle\left(A\right)=\dfrac{6.72^0}{4}=108^o\)

giúp mik nhanh với :<<<

a: Xét tứ giác ABCD có 

\(\widehat{B}+\widehat{C}=180^0\)

nên ABCD là hình thang

Bài 1 :                                                   Bài giải

Ta có : \(\widehat{A}-\widehat{B}=10^o\text{ }\Rightarrow\text{ }\widehat{A}=\widehat{B}+10^o\)

Trong tứ giác ABCD có : 

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

\(\widehat{B}+10+\widehat{B}+60^o+80^o=360^o\)

\(2\widehat{B}+150^o=360^o\)

\(2\widehat{B}=110^o\)

\(\widehat{B}=55^o\text{ }\Rightarrow\text{ }\widehat{A}=65^o\)

Chọn B

a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.

Vì AB//CD, ta có góc ACD = góc BAD.

Vậy số đo góc A là 120 độ.

b) Gọi góc BCD là x độ.

Theo giả thiết, góc B phần góc D = 4/5, ta có:

góc B = (4/5) * góc D

= (4/5) * 60

= 48 độ.

Vì AB//CD, ta có góc BCD = góc BAD.

Vậy góc BAD = góc BCD = x độ.

Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.

Ta có: góc A + góc B + góc C + góc D = 360 độ.

Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:

120 + 48 + góc C + 60 = 360

góc C = 360 - 120 - 48 - 60 = 132 độ.

Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.

* Ib = bài 4

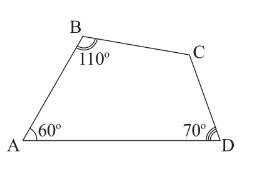
Ta có tổng 4 góc trong tứ giác là: \(360^o\)

\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

Hay: \(60^o+110^o+\widehat{C}+70^o=360^o\)

\(\Rightarrow\widehat{C}=360^o-\left(110^o+60^o+70^o\right)120^o\)

Vậy chọn đáp án A

Chọn A

Đáp án cần chọn là: B

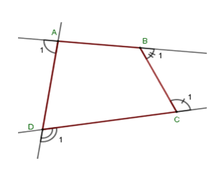
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là  A 1 ^   ;   B 1 ^   ;   C 1 ^   ;   D 1 ^  .

Khi đó ta có :

A ^   +   A 1 ^   = 180 °   ⇒   A 1 ^   =   180 ° - A ^ ;

Theo kết quả các câu trước ta có 

A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^ = 360 ° ⇒ B 1 ^ + C 1 ^ + D 1 ^ = 360 ° - A ^ = 360 ° - 100 ° = 260 °

Vậy  B 1 ^ + C 1 ^ + D 1 ^   =   260 °