CMR:Mx//Py

Những câu hỏi liên quan
Cho biết khối lg của một Oxit của kl là 160 g/ mol , thành phần % m của kl là 70% .Lập công thức hh của oxit và gọi tên kl . Bài làm của mk như sau gọi cthh tổng quát của oxit là AxOy. Biết % m kl là 70% nên - %mO là 30% . Theo đề bài ta có Moxit 160g/mol - klg của mỗi ng tố trong oxit là mA (70*160)/100112g .mO 160-112 48 g Mà Ma*x 112 g - nếu x2 thì MA 112/256 . MO*y 16*y -y 48/163 vậy kl A là Fe và cthh của oxit là Fe2O3
Đọc tiếp
Cho biết khối lg của một Oxit của kl là 160 g/ mol , thành phần % m của kl là 70% .Lập công thức hh của oxit và gọi tên kl . Bài làm của mk như sau gọi cthh tổng quát của oxit là AxOy. Biết % m kl là 70% nên -> %mO là 30% . Theo đề bài ta có Moxit = 160g/mol -> klg của mỗi ng tố trong oxit là mA= (70*160)/100=112g .mO = 160-112= 48 g Mà Ma*x =112 g -> nếu x=2 thì MA = 112/2=56 . MO*y =16*y ->y= 48/16=3 vậy kl A là Fe và cthh của oxit là Fe2O3
Cho hai đường thẳng M và N song song đường thẳng d tạo với đường thẳng m góc bằng 30 độ . Góc tạo bởi đường thẳng n là :
A. 60 độ
B. 160 độ
C. 30 độ
D. 120 độ
Một chất điểm dao động điều hòa trên trục Ox, gia tốc của vật có độ lớn cực đại tại 2 thời điểm liên tiếp là
t
1
5
/
48
s và
t
2
17
/
48
s, vận tốc trung bình (độ biến thiên li độ chia thời gian) trong khoảng thời gian đó là -160 cm/s. Phương trình li độ của vật là A.
x
...
Đọc tiếp
Một chất điểm dao động điều hòa trên trục Ox, gia tốc của vật có độ lớn cực đại tại 2 thời điểm liên tiếp là t 1 = 5 / 48 s và t 2 = 17 / 48 s, vận tốc trung bình (độ biến thiên li độ chia thời gian) trong khoảng thời gian đó là -160 cm/s. Phương trình li độ của vật là
A. x = 10 cos ( 8 πt + π / 2 ) cm
B. x = 20 cos ( 4 πt + π / 2 ) cm
C. x = 10 cos ( 8 πt ) c m
D. x = 20 cos ( 4 πt - 5 π / 2 ) cm
Chọn D.

Thời gian hai lần liên tiếp gia tốc của vatah có độ lớn cực đại (vật ở vị trí biên) là T/2 nên:
![]()
suy ra:
![]()
Vận tốc trung bình trong khoảng thời gian này
![]()
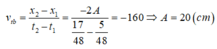
Từ t = 0 đến t 1 = 5 / 48 s phải quét một góc:
![]()
Vì tại thời điểm , vật ở biên dương nên từ vị trí này quay ngược lại một góc thì được trạng thái ban đầu và lúc này, pha ban đầu của dao động
![]()
![]()
Đúng 0
Bình luận (0)
Đổi:
a.60 độ C ra đơn vị độ F ?
b. 112 độ F ra đơn vị độ C ?
c. 30 độ C ra đơn vị độ F ?
d. 50 độ F ra đơn vị độ C ?
trình bày cách làm nhé
a, \(\left(60^oC.1,8\right)+32=140^oF\)
b, \(\left(112^oF-32\right):1,8\approx44,4^oC\)
c, \(\left(30^oC.1,8\right)+32=86^oF\)
d, \(\left(50^oF-32\right):1,8=10^oC\)
Đúng 0
Bình luận (4)
bài 1:tìm 3 số x,y,z tỉ lệ nghịch với các số -5;2;7 biết 2x+y-z =48
bài 2:vẽ đồ thị hàm số y=-2.5x và y=3 trên cùng hệ trục tọa độ . tìm tọa độ giao điểm của 2 đồ thị trên
Bài 1:
Vì \(x,y,z\) tỉ lệ nghịch với các số \(-5;2;7\)
\(\Rightarrow-5x=2y=7z\)
\(\Rightarrow\) \(\dfrac{-5x}{70}=\dfrac{2y}{70}=\dfrac{7z}{70}\)
\(\Rightarrow\dfrac{x}{-14}=\dfrac{y}{35}=\dfrac{z}{10}\)
\(\Rightarrow\dfrac{2x}{-28}=\dfrac{y}{35}=\dfrac{z}{10}\)
Áp dụng t/c dãy tỉ số = nhau ta có:
\(\Rightarrow\dfrac{2x}{-28}=\dfrac{y}{35}=\dfrac{z}{10}=\dfrac{2x+y-z}{-28+35-10}=\dfrac{48}{-3}=-16\)
Khi đó \(\left[{}\begin{matrix}\dfrac{2x}{-28}=-16\\\dfrac{y}{35}=-16\\\dfrac{z}{10}=-16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=224\\y=-560\\z=-160\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=224\\y=-560\\z=-160\end{matrix}\right.\).
Đúng 0
Bình luận (0)
một dây dẫn, khi dòng điện có cường độ I11,4A đi qua thì nóng lên đến nhiệt độ t155oC; khi dòng điện có cường độ I22,8A đi qua thì nóng đến nhiệt độ t2160oC. Coi nhiệt lượng tỏa ra môi trường xung quanh tỉ lệ thuận với độ chênh lệch nhiệt độ giữa dây và môi trường. Nhiệt độ môi trường không đổi. Bỏ qua sự thay đổi của điện trở theo nhiệt độ. Tìm nhiệt độ của dây dẫn kì dòng điện có cường độ la I35,6A đi qua
Đọc tiếp
một dây dẫn, khi dòng điện có cường độ I1=1,4A đi qua thì nóng lên đến nhiệt độ t1=55oC; khi dòng điện có cường độ I2=2,8A đi qua thì nóng đến nhiệt độ t2=160oC. Coi nhiệt lượng tỏa ra môi trường xung quanh tỉ lệ thuận với độ chênh lệch nhiệt độ giữa dây và môi trường. Nhiệt độ môi trường không đổi. Bỏ qua sự thay đổi của điện trở theo nhiệt độ. Tìm nhiệt độ của dây dẫn kì dòng điện có cường độ la I3=5,6A đi qua
Cho hình 2, B4= 48 độ, A3= 132 độ. Chứng minh m//n.
ta có góc B4 + góc A3=180 độ (mà hai góc này ở vị trí trong cùng phía)
=> m//h <đpcm>
Đúng 1
Bình luận (4)
trong mặt phẳng tọa độ Oxy, cho đường thẳng (d):y =2x-a+1 và parabol (P) :y =\(\dfrac{1}{2}x^2\)
tìm a để (d) cắt (P) tại hai điểm phận biệt có tọa độ (x1,y1) và (x2,y2) thỏa mãn điều kiện x1x2(y1+y2) +48=0
PTHĐGĐ là:
1/2x^2=2x-a+1
=>x^2=4x-2a+2
=>x^2-4x+2a-2=0
Δ=(-4)^2-4(2a-2)
=16-8a+8=-8a+24
Để (d) cắt (P) tại hai điểm phân biệt thì -8a+24>0
=>-8a>-24
=>a<3
x1x2(y1+y2)+48=0
=>(2a-2)*[(x1)^2+(x2)^2]+48=0
\(\Leftrightarrow\left(2a-2\right)\cdot\left[4^2-2\left(2a-2\right)\right]+48=0\)
=>\(\left(2a-2\right)\left(16-4a+4\right)+48=0\)
=>\(\left(2a-2\right)\left(-4a+20\right)+48=0\)
=>\(2\left(a-2\right)\cdot\left(-4\right)\cdot\left(a-5\right)+48=0\)
=>(a-2)(a-5)=-48/-8=6
=>a^2-7a+10-6=0
=>a^2-7a+4=0
=>\(a=\dfrac{7\pm\sqrt{33}}{2}\)
Đúng 0
Bình luận (0)
Cho độ tan của CuSO4 tại 27 độ C là 48,4 g và tại 48 độ C là 54,2 g. Đun nóng 134 g dd CuSO4 bão hòa ở 27 độ C lên 48 độ C . Cần thêm bao nhiêu g CuSO4 vào dd để thu được dd bão hòa tại 48 độ C ?






















