trong các tập sau, tập nào là con tập nào?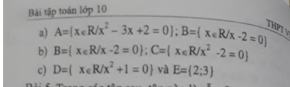

Những câu hỏi liên quan
Trong các tập sau, tập nào là tập con của tập nào?
A = { 1; 2; 3 } B = { \(x\in N\) | x < 4 }
C = ( 0; \(+\infty\) ) D = { \(x\in R\) | \(2x^2-7x+3=0\) }
Ta có:
\(A=\left\{1;2;3\right\}\)
\(B=\left\{x\in N|x< 4\right\}\)
\(\Rightarrow B=\left\{...;0;1;2;3\right\}\)
\(C=\left\{0;+\infty\right\}\)
\(\Rightarrow\text{C}\text{ }=\left\{x>0;x\in R\right\}\)
\(D=\left\{x\in R|2x^2-7x+3=0\right\}\)
\(\Rightarrow D=\left\{3;\dfrac{1}{2}\right\}\)
Nên A là con của B và C; D là con của C
Đúng 2
Bình luận (0)
cho tập hợp M=1,2,3,4,5,6,trong các tập hợp sau,tập hợp nào là tập hợp con của M
Cho tập hợp X = {1;2;4;7}. Trong các tập hợp sau, tập hợp nào là tập hợp con của tập hợp X?
a, {1;7}
b, {1;5}
c, {2;5}
d, {3;7}
Trong các tập hợp sau, tập hợp nào có 32 tập hợp con?
A. A = {-2; 3; 5; 12}.
B. B = {-1; 0; 2; 4; 9}.
C. C = {-5; 0; 1; 4}.
D. D = {-3; -1; 0; 3; 6; 11}.
Đáp án: B
Số tập hợp con của tập hợp có n phần tử là 2n = 32 ⇒ n = 5. Chỉ có tập hợp B là tập hợp có 5 phần tử.
Đúng 0
Bình luận (0)
Trong các tập sau, tập hợp nào có đúng một tập hợp con?
A. ∅
B. {a}
C. {a;b}
D. ∅ ; A với A là một tập hợp khác rỗng
2 Cho tập hợp M={1;2;3}. Trong các tập hợp sau tập hợp nào là tập hợp con của M
M1={0;1} B. M2={0;2} C. M3={3;4} D. M4={1;3}
Xem thêm câu trả lời
Trong các tập hợp sau đây, tập nào là tập rỗng:
a/A={x ∈ Z | |x| < 1}
b/B={x ∈ R | x2 - x + 1= 0}
c/C={x ∈ N | x2 + 7x + 12 = 0}
Cho tập hợp A ={1;2;3}
a/ Viết tất cả các tập hợp con gồm 2 phần tử của tập hợp A
b/ Viết tất cả các tập hợp con của tập hợp A
Tìm tất cả các tập X sao cho{1;3} ⊂ X ⊂{1;2;3;4;5}
Tập hợp C rỗng vì \(x^2+7x+12=0\Leftrightarrow x\in\left\{-3;-4\right\}\notin N\)
\(a,\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\}\\ b,\left\{1\right\};\left\{2\right\};\left\{3\right\};\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\};\left\{1;2;3\right\}\)
\(X=\left\{1;3\right\}\\ X=\left\{1;2;3\right\}\\ X=\left\{1;3;4\right\}\\ X=\left\{1;3;5\right\}\\ X=\left\{1;2;3;4\right\}\\ X=\left\{1;2;3;5\right\}\\ X=\left\{1;3;4;5\right\}\\ X=\left\{1;2;3;4;5\right\}\)
Đúng 1
Bình luận (0)
Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?a) A { - sqrt 3 ;sqrt 3 } và B { x in mathbb{R}|{x^2} - 3 0} b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;c) E { x in mathbb{N}|x là ước của 12} và F { x in mathbb{N}|x là ước của 24} .Viết tất cả các tập con của tập hợp A { a;b} .
Đọc tiếp
Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?
a) \(A = \{ - \sqrt 3 ;\sqrt 3 \} \) và \(B = \{ x \in \mathbb{R}|{x^2} - 3 = 0\} \)
b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;
c) \(E = \{ x \in \mathbb{N}|x\) là ước của 12\(\} \) và \(F = \{ x \in \mathbb{N}|x\) là ước của 24\(\} .\)
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
a) A là tập con củ B vì:
\( - \sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( { - \sqrt 3 } \right)^2} - 3 = 0\), nên \( - \sqrt 3 \in B\)
\(\sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( {\sqrt 3 } \right)^2} - 3 = 0\), nên \(\sqrt 3 \in B\)
Lại có: \({x^2} - 3 = 0 \Leftrightarrow x = \pm \sqrt 3 \) nên \(B = \{ - \sqrt 3 ;\sqrt 3 \} \).
Vậy A = B.
b) C là tập hợp con của D vì: Mỗi tam giác đều đều là một tam giác cân.
\(C \ne D\) vì có nhiều tam giác cân không là tam giác đều, chẳng hạn: tam giác vuông cân.
c) E là tập con của F vì \(24\; \vdots \;12\) nên các ước nguyên dương của 12 đều là ước nguyên dương của 24.
\(E \ne F\) vì \(24 \in F\)nhưng \(24 \notin E\)
Đúng 0
Bình luận (0)
Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập còn lại? Chúng có bằng nhau không?
a) \(A = \{ x \in \mathbb{N}|\;x < 2\} \) và \(B = \{ x \in \mathbb{R}|\;{x^2} - x = 0\} \)
b) C là tập hợp các hình thoi và D là tập hợp các hình vuông
c) \(E = ( - 1;1]\) và \(F = ( - \infty ;2]\)
a) \(A = \{ x \in \mathbb{N}|\;x < 2\} = \{ 0;1\} \) và \(B = \{ x \in \mathbb{R}|\;{x^2} - x = 0\} = \{ 0;1\} \)
Vậy A = B, A là tập con của tập B và ngược lại.
b) D là tập hợp con của C vì: Mỗi hình vuông đều là một hình thoi đặc biệt: hình thoi có một góc vuông.
\(C \ne D\) vì có nhiều hình thoi không là hình vuông, chẳng hạn:
c) \(E = ( - 1;1] = \left\{ {x \in \mathbb{R}|\; - 1 < x \le 1} \right\}\) và \(F = ( - \infty ;2] = \left\{ {x \in \mathbb{R}|\;x \le 2} \right\}\)
E là tập con của F vì \( - 1 < x \le 1 \Rightarrow x \le 2\) .
\(E \ne F\) vì \( - 3 \in F\)nhưng \( - 3 \notin E\)
Đúng 0
Bình luận (0)



















