Dựng 1 hình vuông với 1 lần dùng compa

Những câu hỏi liên quan
Dựng hình vuông bằng 1 lần dùng compa và không hạn chế số lần dùng thướt thẳng(không có số đo)
Dễ vẽ 1 đường tròn . Đường kính
Lấy 1 điểm trên đg tròn nối điểm đó với hai đầu đg kính
Đúng 0
Bình luận (0)
cho một góc 19 độ dùng thước và compa dựng góc 1 độ
1. Từ thước và compa, và góc 19 độ có sẵn, ta dựng lại được góc 19 độ.
2. ghép góc 19 độ liên tiếp 19 lần quang gốc tạo độ tạo thành 19* 19 =361 độ, trừ cho góc 360 độ, thành 1 độ
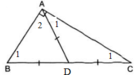
Lấy ba điểm A, B, C bất kỳ, không thẳng hàng
Vẽ các đoạn thẳng AB, BC, CA.
a) Dùng compa để dựng đoạn MP = AB + BC
b) Dùng compa để so sánh AC với AB + BC
b) Áp dụng bđt tam giác vào ΔABC, ta được:
AB+BC>AC
Đúng 1
Bình luận (0)
Lấy 3 điểm A,B,C không thẳng hàng.Vẽ các đoạn thẳng AB,BC,CA.
a)Dùng compa để dựng đoạn MP=AB+BC
b)Dùng compa so sánh AC với AB+BC
Lấy ba điểm A, B, C bất kì, không thẳng hàng .Vẽ các đoạn AB, BC, CA
a) Dùng compa để dựng đoạn MP = AB = BC
b) Dùng compa để so sánh AC với AB = BC
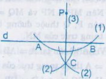
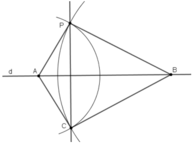
Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P vuông góc với đường thẳng d bằng thước và compa như sau: (1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó có cắt d tại hai điểm A và B. (2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C (C ≠ P) (3) Vẽ đường thẳng PC. Em hãy chứng minh đường thẳng PC vuông góc với d. Đố: Tìm thêm một cách dựng nữa (bằng thước và compa...
Đọc tiếp
Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P vuông góc với đường thẳng d bằng thước và compa như sau:
(1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó có cắt d tại hai điểm A và B.
(2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C (C ≠ P)
(3) Vẽ đường thẳng PC.
Em hãy chứng minh đường thẳng PC vuông góc với d.
Đố: Tìm thêm một cách dựng nữa (bằng thước và compa)
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
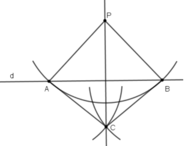
QUẢNG CÁOb) Một cách vẽ khác
- Lấy hai điểm A, B bất kì trên d.
- Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
- Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.
Chứng minh :
- Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.
Đúng 0
Bình luận (0)
Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại A.
Ứng dụng: Một tờ giấy bị rách mép (h.65). Hãy dùng thước và compa dựng đường vuông góc với cạnh AB tại A.
Quan sát hình thoi ở hình 4.10a.
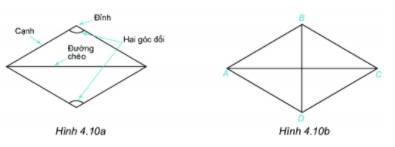
1.Dùng thước thẳng hoặc compa so sánh các cạnh của hình thoi (h.4.10b).
2. Kiểm tra xem hai đường chéo của hình thoi có vuông góc với nhau không?
3. Các cạnh đổi của hình thoi có song song với nhau không?
4. Các góc đối của hình thoi có bằng nhau không?
1) Dùng thước thẳng hoặc compa, ta được: AB = BC = CD = AD. Vậy các cạnh của hình thoi bằng nhau.
2) Dùng eke ta thấy AC vuông góc với BD. Vậy hai đường chéo của hình thoi vuông góc với nhau.
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình thoi song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình thoi ABCD bằng nhau.
Đúng 2
Bình luận (0)
dùng thước eke để vẽ hình vuông cạnh 7cm vào vở,kẻ thêm hai đường chéo rồi dùng compa đo và so sánh độ dài của chúng