\(\sin\widehat{A}=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)

\(\cot\widehat{A}=\dfrac{5}{13}:\dfrac{12}{13}=\dfrac{5}{12}\)

\(\tan\widehat{B}=\dfrac{5}{12}\)

Lời giải:

Ta có:

$\frac{5}{13}=\cos A=\frac{AC}{AB}$

$\Rightarrow AB=\frac{13}{5}AC$

Áp dụng định lý Pitago:

$AC^2+BC^2=AB^2$

$\Leftrightarrow AC^2+10^2=(\frac{13}{5}AC)^2$
$\Leftrightarrow 100=\frac{144}{25}AC^2$
$\Leftrightarrow AC^2=\frac{625}{36}$

$\Rightarrow AC=\frac{25}{6}$ (cm) 

Vậy......

Hình vẽ:

\(a,cosC=\dfrac{5}{13}\\ Ta,có:cos^2C+sin^2C=1\\ \Rightarrow sinC=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\\ cosB+sinC=1\\ \Leftrightarrow cosB+\dfrac{12}{13}=1\\ \Rightarrow cosB=\dfrac{1}{13}\\ tanC=\dfrac{sinC}{cosC}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)

\(b,tanB=\dfrac{1}{5}\Rightarrow\dfrac{sinB}{cosB}=\dfrac{1}{5}\Rightarrow cosB=5sinB\\ E=\dfrac{sinB-3cosB}{2sinB+3cosB}=\dfrac{sinB-3.5.sinB}{2sinB+3.5.sinB}=\dfrac{-14sinB}{17sinB}=-\dfrac{14}{17}\)

\(\sin^2\widehat{A}+\cos^2\widehat{A}=1\Leftrightarrow\cos^2\widehat{A}=1-\left(\dfrac{3}{5}\right)^2=1-\dfrac{9}{25}=\dfrac{16}{25}\\ \Leftrightarrow\cos\widehat{A}=\dfrac{4}{5}\\ \tan\widehat{A}=\dfrac{\sin\widehat{A}}{\cos\widehat{A}}=\dfrac{3}{4}\\ \Rightarrow\cot\widehat{A}=\dfrac{1}{\tan\widehat{A}}=\dfrac{4}{3}\)

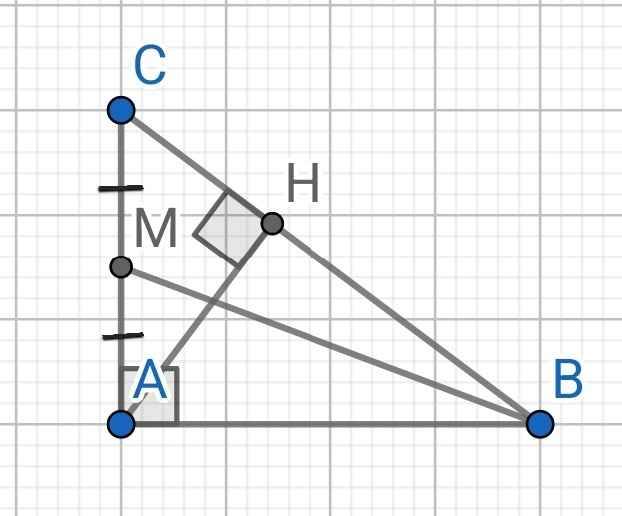
\(tanB=\dfrac{AC}{AB}=\dfrac{5}{12}\)

⇒ AC = \(\dfrac{5}{12}\) .AB

= \(\dfrac{5}{12}.5\)

\(=\dfrac{25}{12}\) (cm)

∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

\(=5^2+\left(\dfrac{25}{12}\right)^2\)

= \(\dfrac{4225}{144}\)

⇒ BC = \(\dfrac{65}{12}\) (cm)

AH.BC = AB.AC

⇒ AH = AB . AC : BC

= 5 . \(\dfrac{25}{12}:\dfrac{65}{12}\)

\(=\dfrac{25}{13}\left(cm\right)\)

M là trung điểm của AC

⇒ AM = AC : 2 = \(\dfrac{25}{12}:2\) \(=\dfrac{25}{24}\) (cm)

∆ABM vuông tại A

⇒ BM² = AB² + AM²

= \(5^2+\left(\dfrac{25}{24}\right)^2\)

= \(\dfrac{15025}{576}\)

⇒ BM = \(\dfrac{5\sqrt{601}}{24}\) (cm)

\(\tan B=\sqrt{2}\Leftrightarrow\dfrac{\sin B}{\cos B}=\sqrt{2}\Leftrightarrow\sin B=\sqrt{2}\cos B\\ \sin^2B+\cos^2B=1\Leftrightarrow3\cos^2B=1\\ \Leftrightarrow\cos B=\sqrt{\dfrac{1}{3}}=\dfrac{\sqrt{3}}{3}\\ \Leftrightarrow\sin B=\dfrac{\sqrt{6}}{3}\\ \Leftrightarrow\left\{{}\begin{matrix}\sin C=\cos B=\dfrac{\sqrt{3}}{3}\\\cos C=\sin B=\dfrac{\sqrt{6}}{3}\end{matrix}\right.\\ \cot C=\tan B=\sqrt{3};\tan C=\dfrac{1}{\cot C}=\dfrac{\sqrt{3}}{3}\)