Cho hình vuông ABCD cạnh a. M là trung điểm BC, N thuộc AC và AC= 1/3 AN. Tính độ dài \(\overrightarrow{DM},\overrightarrow{AN},\overrightarrow{MN}\)

Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.
a) Biểu thị các vecto \(\overrightarrow {DM} ,\overrightarrow {AN} \) theo các vecto \(\overrightarrow {AB} ,\overrightarrow {AD} \)
b) Tính \(\overrightarrow {DM} .\overrightarrow {AN} \) và tìm góc giữa hai đường thẳng DM và AN.
a) Ta có:
\(\overrightarrow {DM} = \overrightarrow {DA} + \overrightarrow {AM} = - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} \) (do M là trung điểm của AB)
\(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) (do N là trung điểm của BC)
b)
\(\begin{array}{l}\overrightarrow {DM} .\overrightarrow {AN} = \left( { - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} } \right).\left( {\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} } \right)\\ = - \overrightarrow {AD} .\overrightarrow {AB} - \frac{1}{2}{\overrightarrow {AD} ^2} + \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{1}{4}\overrightarrow {AB} .\overrightarrow {AD} \end{array}\)
Mà \(\overrightarrow {AB} .\overrightarrow {AD} = \overrightarrow {AD} .\overrightarrow {AB} = 0\) (do \(AB \bot AD\)), \({\overrightarrow {AB} ^2} = A{B^2} = {a^2};{\overrightarrow {AD} ^2} = A{D^2} = {a^2}\)
\( \Rightarrow \overrightarrow {DM} .\overrightarrow {AN} = - 0 - \frac{1}{2}{a^2} + \frac{1}{2}{a^2} + \frac{1}{4}.0 = 0\)
Vậy \(DM \bot AN\) hay góc giữa hai đường thẳng DM và AN bằng \({90^ \circ }\).
Đúng 0
Bình luận (0)
Cho tam giác ABC đều cạnh a. M và N là các điểm sao cho 3overrightarrow{BM} 2overrightarrow{BC}, 5overrightarrow{AN} 4overrightarrow{AC}a, tính overrightarrow{AB}.overrightarrow{AC}; overrightarrow{BC}.overrightarrow{AC}b, cm AM vuông góc BN
Đọc tiếp
Cho tam giác ABC đều cạnh a. M và N là các điểm sao cho 3\(\overrightarrow{BM}\)= 2\(\overrightarrow{BC}\), 5\(\overrightarrow{AN}\) = 4\(\overrightarrow{AC}\)
a, tính \(\overrightarrow{AB}\).\(\overrightarrow{AC}\); \(\overrightarrow{BC}\).\(\overrightarrow{AC}\)
b, cm AM vuông góc BN
Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD. Chứng minh rằng:
a) \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
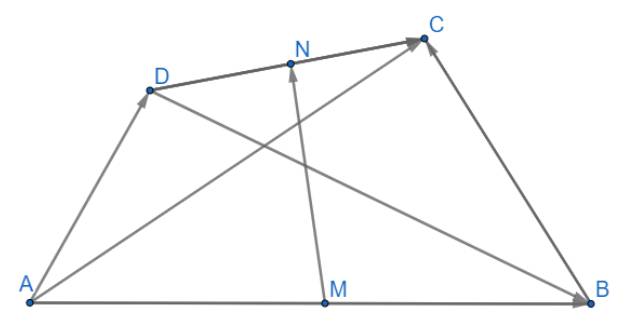
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \\= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \) (đpcm)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
\(\)\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} \)
Mặt khác ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
Suy ra \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cách 2:
\(\begin{array}{l}
\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \\
\Leftrightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \\
\Leftrightarrow \overrightarrow {DC} = \overrightarrow {DC} (đpcm)
\end{array}\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:
a) \(\overrightarrow {DA} + \overrightarrow {DC} \)
b) \(\overrightarrow {AB} - \overrightarrow {AD} \)
c) \(\overrightarrow {OA} + \overrightarrow {OB} \) với O là giao điểm của AC và BD.
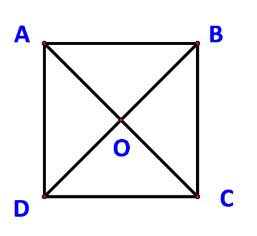
a) Do ABCD cũng là một hình bình hành nên \(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \)
\( \Rightarrow \;|\overrightarrow {DA} + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2 \)
b) Ta có: \(\overrightarrow {AD} + \overrightarrow {DB} = \overrightarrow {AB} \) \( \Rightarrow \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2 \)
c) Ta có: \(\overrightarrow {DO} = \overrightarrow {OB} \)
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {DO} = \overrightarrow {DO} + \overrightarrow {OA} = \overrightarrow {DA} \)
\( \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.\)
Đúng 0
Bình luận (0)
Cho ΔABC . Các điểm M ,N , P lần lượt là trung điểm AB , AC , BC .
Xác định hiệu \(\overrightarrow{AM}-\overrightarrow{AN}\), \(\overrightarrow{MN}-\overrightarrow{NC}\), \(\overrightarrow{MN}-\overrightarrow{PN}\), \(\overrightarrow{BP}-\overrightarrow{CP}\)
\(\overrightarrow{AM}-\overrightarrow{AN}=\overrightarrow{NM}\)
\(\overrightarrow{MN}-\overrightarrow{NC}=\overrightarrow{CM}\)
Đúng 1
Bình luận (0)
Câu 1: Cho hình vuông ABCD có cạnh bằng 1. Gọi O là giao điểm 2 đường chéo AC, BD. Tìm khẳng định sai:
A. overrightarrow{AB}.overrightarrow{BC}0
B.overrightarrow{BC}.overrightarrow{BD}1
C.overrightarrow{OD}.overrightarrow{OB}-frac{1}{2}
D. overrightarrow{AB}.overrightarrow{AC}sqrt{2}
Câu 2: Cho tam giác ABC có M là trung điểm BC, N là trung điểm của BM. Đẳng thức nào sau đây đúng?
A. 4overrightarrow{AN}3overrightarrow{AB}+overrightarrow{AC}
B, 2overrightarrow{AN}3overrightarrow{AB}+overright...
Đọc tiếp
Câu 1: Cho hình vuông ABCD có cạnh bằng 1. Gọi O là giao điểm 2 đường chéo AC, BD. Tìm khẳng định sai:
A. \(\overrightarrow{AB}.\overrightarrow{BC}=0\)
B.\(\overrightarrow{BC}.\overrightarrow{BD}=1\)
C.\(\overrightarrow{OD}.\overrightarrow{OB}=-\frac{1}{2}\)
D. \(\overrightarrow{AB}.\overrightarrow{AC}=\sqrt{2}\)
Câu 2: Cho tam giác ABC có M là trung điểm BC, N là trung điểm của BM. Đẳng thức nào sau đây đúng?
A. \(4\overrightarrow{AN}=3\overrightarrow{AB}+\overrightarrow{AC}
\)
B, \(2\overrightarrow{AN}=3\overrightarrow{AB}+\overrightarrow{AC}\)
C.\(4\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{3AC}\)
D.\(4\overrightarrow{AN}=3\overrightarrow{AB}+2\overrightarrow{AC}\)
Câu 1:
\(AC=\sqrt{AB^2+BC^2}=\sqrt{2}\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos45^0=1.\sqrt{2}.\frac{\sqrt{2}}{2}=1\)
Đáp án D sai
Câu 2:
\(BN=\frac{1}{2}BM=\frac{1}{4}BC\Rightarrow4\overrightarrow{BN}=\overrightarrow{BC}\)
Ta có:
\(4\overrightarrow{AN}=4\left(\overrightarrow{AB}+\overrightarrow{BN}\right)=4\overrightarrow{AB}+4\overrightarrow{BN}=4\overrightarrow{AB}+\overrightarrow{BC}\)
\(=4\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AC}=4\overrightarrow{AB}-\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AB}+\overrightarrow{AC}\)
Đáp án A đúng
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)
Ta có:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \)
Mặt khác: \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \)
\(\begin{array}{l} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} + \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \\ \Leftrightarrow 2\overrightarrow {MN} = \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {CN} } \right) + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow {BC} + \overrightarrow {AD} \end{array}\)
Lại có:
\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BD} + \overrightarrow {DC} + \overrightarrow {AD} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {BD} .\)
Vậy \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD tâm O, cạnh bằng 1. Gọi M là điểm trên cạnh AB sao cho BM = 2MA; N trên AC sao cho AN = 3NC. Tích vô hướng của \(\overrightarrow{MN}.\overrightarrow{DN}\) bằng:
A. \(-\dfrac{1}{8}\)
B. \(\dfrac{1}{9}\)
C. \(\dfrac{1}{8}\)
D. \(\dfrac{3}{4}\)
\(BM=2MA\Rightarrow\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}\); \(AN=3NC\Rightarrow\overrightarrow{AN}=\dfrac{3}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\)
Do đó:
\(\overrightarrow{MN}.\overrightarrow{DN}=\left(\overrightarrow{MA}+\overrightarrow{AN}\right)\left(\overrightarrow{DA}+\overrightarrow{AN}\right)\)
\(=\left(-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\right)\left(-\overrightarrow{AD}+\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\right)\)
\(=\left(\dfrac{5}{12}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\right)\left(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\right)\)
\(=\dfrac{5}{16}AB^2-\dfrac{3}{16}AD^2=\dfrac{1}{8}AB^2=\dfrac{1}{8}\) (chú ý rằng \(\overrightarrow{AB}.\overrightarrow{AD}=0\) và \(AB=AD=1\))
Đúng 0
Bình luận (0)
Cho tam giác ABC có widehat{BAC}60^0;AB4;AC6
a) Tính tích vô hướng overrightarrow{AB}.overrightarrow{AC};overrightarrow{AB}.overrightarrow{BC}, độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác ABC
b) Lấy các điểm M, N định bởi : 2overrightarrow{AM}+3overrightarrow{MC}overrightarrow{0};overrightarrow{NB}+xoverrightarrow{BC}overrightarrow{0};left(xne-1right). Định x để AN vuông góc với BM ?
Đọc tiếp
Cho tam giác ABC có \(\widehat{BAC}=60^0;AB=4;AC=6\)
a) Tính tích vô hướng \(\overrightarrow{AB}.\overrightarrow{AC};\overrightarrow{AB}.\overrightarrow{BC}\), độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác ABC
b) Lấy các điểm M, N định bởi : \(2\overrightarrow{AM}+3\overrightarrow{MC}=\overrightarrow{0};\overrightarrow{NB}+x\overrightarrow{BC}=\overrightarrow{0};\left(x\ne-1\right)\). Định \(x\) để AN vuông góc với BM ?














