a: M,N,P đều nằm trên trục tung

b; Hoành độ bằng 0

a, Ta có : \(AB=OA-OB=a-b\left(cm\right)\)

b, Có lẽ là M trên tia Ox .

Ta có : \(OM=\dfrac{1}{2}\left(a+b\right)\)

=> M là trung điểm của AB .

Mình làm rõ ý B hơn để bạn dễ hiểu nha

Thấy : \(OM=\dfrac{1}{2}\left(a+b\right)< \dfrac{1}{2}\left(a+a\right)\)

\(\Rightarrow OM< OA\)

\(\Rightarrow OM=OA-AM\)

\(\Rightarrow\dfrac{1}{2}\left(a+b\right)=a-AM\)

\(\Leftrightarrow AM=a-\dfrac{1}{2}\left(a+b\right)=a-\dfrac{1}{2}a-\dfrac{1}{2}b=\dfrac{1}{2}\left(a-b\right)\)

=> Khoảng cách từ M đến A bằng nửa khoảng cách từ B đến A .

=> M là trung điểm của AB .

Vậy ...

Bn tk nha:🌱☘️

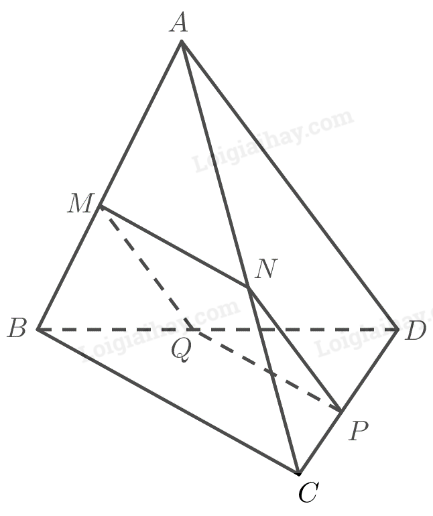
a) Ta có:

\(\begin{array}{l}MN = \left( \alpha  \right) \cap \left( {ABC} \right)\\PQ = \left( \alpha  \right) \cap \left( {BC{\rm{D}}} \right)\\BC = \left( {ABC} \right) \cap \left( {BC{\rm{D}}} \right)\\MN\parallel BC\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel PQ\parallel BC\) (1).

\(\begin{array}{l}MQ = \left( \alpha  \right) \cap \left( {ABD} \right)\\NP = \left( \alpha  \right) \cap \left( {AC{\rm{D}}} \right)\\A{\rm{D}} = \left( {ABD} \right) \cap \left( {AC{\rm{D}}} \right)\\MQ\parallel A{\rm{D}}\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MQ\parallel NP\parallel A{\rm{D}}\) (2).

Từ (1) và (2) suy ra \(MNPQ\) là hình bình hành.

b) Để \(MNPQ\) là hình thoi thì \(MN = NP\).

Ta có:

\(\begin{array}{l}MN\parallel BC \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\\NP\parallel A{\rm{D}} \Rightarrow \frac{{NP}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}} \Rightarrow \frac{{MN}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}}\end{array}\)

Ta có:

\(\begin{array}{l}\frac{{AN}}{{AC}} + \frac{{CN}}{{AC}} = 1 \Leftrightarrow \frac{{MN}}{{BC}} + \frac{{MN}}{{A{\rm{D}}}} = 1 \Leftrightarrow MN.\left( {\frac{1}{{BC}} + \frac{1}{{A{\rm{D}}}}} \right) = 1\\ \Leftrightarrow MN.\frac{{BC + A{\rm{D}}}}{{BC.A{\rm{D}}}} = 1 \Leftrightarrow MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\end{array}\)

Vậy nếu \(MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\) thì \(MNPQ\) là hình thoi.

Sửa đề: Sao cho biểu thức T đạt GTLN

Phương trình hoành độ giao điểm là:

\(\dfrac{1}{2}x^2=\left(m+1\right)x-m^2-\dfrac{1}{2}\)

=>\(\dfrac{1}{2}x^2-\left(m+1\right)x+m^2+\dfrac{1}{2}=0\)

=>\(x^2-\left(2m+2\right)x+2m^2+1=0\)

\(\text{Δ}=\left(2m+2\right)^2-4\left(2m^2+1\right)\)

\(=4m^2+8m+4-8m^2-4=-4m^2+8m\)

Để phương trình có hai nghiệm thì Δ>=0

=>\(-4m^2+8m>=0\)

=>\(-4\left(m^2-2m\right)>=0\)

=>\(m^2-2m< =0\)

=>\(m\left(m-2\right)< =0\)

TH1: \(\left\{{}\begin{matrix}m>=0\\m-2< =0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m>=0\\m< =2\end{matrix}\right.\)

=>0<=m<=2

TH2: \(\left\{{}\begin{matrix}m< =0\\m-2>=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m< =0\\m>=2\end{matrix}\right.\)

=>Loại

\(\dfrac{1}{2}x^2-\left(m+1\right)x+m^2+\dfrac{1}{2}=0\)

\(a=\dfrac{1}{2};b=-\left(m+1\right);c=m^2+\dfrac{1}{2}\)

Theo Vi-et, ta có: 

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{m+1}{\dfrac{1}{2}}=2\left(m+1\right)\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{m^2+\dfrac{1}{2}}{\dfrac{1}{2}}=2\left(m^2+\dfrac{1}{2}\right)=2m^2+1\end{matrix}\right.\)

\(T=y_1+y_2-x_1x_2-\left(x_1+x_2\right)\)

\(=\dfrac{1}{2}x_1^2+\dfrac{1}{2}x_2^2-2m^2-1-2m-2\)

\(=\dfrac{1}{2}\left(x_1^2+x_2^2\right)-2m^2-2m-3\)

\(=\dfrac{1}{2}\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-2m^2-2m-3\)

\(=\dfrac{1}{2}\left[\left(2m+2\right)^2-2\left(2m^2+1\right)\right]-2m^2-2m-3\)

\(=\dfrac{1}{2}\left[4m^2+8m+4-4m^2-2\right]-2m^2-2m-3\)

\(=\dfrac{1}{2}\left(8m+2\right)-2m^2-2m-3\)

\(=4m+1-2m^2-2m-3=-2m^2+2m-2\)

\(=-2\left(m^2-m+1\right)\)

\(=-2\left(m^2-m+\dfrac{1}{4}+\dfrac{3}{4}\right)\)

\(=-2\left[\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]\)

\(=-2\left(m-\dfrac{1}{2}\right)^2-\dfrac{3}{2}< =-\dfrac{3}{2}\)

Dấu '=' xảy ra khi m=1/2

Lời giải:
PT hoành độ giao điểm:

$\frac{1}{2}x^2-(m+1)x+m^2+\frac{1}{2}=0$

$\Leftrightarrow x^2-2(m+1)x+2m^2+1=0(*)$

Để 2 đths cắt nhau tại 2 điểm pb thì pt $(*)$ phải có 2 nghiệm pb

$\Leftrightarrow \Delta'=(m+1)^2-(2m^2+1)>0$

$\Leftrightarrow m(2-m)>0$

$\Leftrightarrow 0< m< 2$
Áp dụng định lý Viet:

$x_1+x_2=2m+2$
$x_1x_2=2m^2+1$
Khi đó:

$T=y_1+y_2-x_1x_2-(x_1+x_2)$

$=\frac{1}{2}(x_1^2+x_2^2)-x_1x_2-(x_1+x_2)$

$=\frac{1}{2}(x_1+x_2)^2-2x_1x_2-(x_1+x_2)$

$=\frac{1}{2}(2m+2)^2-2(2m^2+1)-(2m+2)$

$=-2m^2+2m-2$

Với điều kiện $0< m< 2$ thì biểu thức này không có min nhé. Bạn xem lại.

Giả sử M có tọa độ (x;y), ta có:

MA²= (x - 1)² + (y + 2)² ;

MA²= (x + 3)² + (y - 1)²

MC²= (x - 4)² + (y + 2)²

Vì MA² + MB² = MC² nên x² + y² + 12x - 10y - 5 = 0.

Vậy { M } là đường tròn tâm I (-6;5), bán kính R = \(\sqrt{66}\)