undefined hình ảnh r

ảnh đâu ?

Ảnh đÂu Mà GiÚP ?

a, Xét tam giác ABD và tam giác BDC ta có : 

^BAD = ^CBD ( gt )

^ABD = ^BDC ( so le trong )

Vậy tam giác ABD ~ tam giác BDC ( g.g )

\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\)( tỉ số đồng dạng ) \(\Rightarrow BD^2=AB.DC=4.9=36\)

\(\Rightarrow BD=\sqrt{36}=6\)cm 

b, Gọi giao điểm AC và BD là I

Xét tam giác BIE và tam giác AID có : BE // AD 

Theo hệ quả Ta lét ta có : \(\frac{BI}{ID}=\frac{IE}{IA}=\frac{BE}{AD}\)

Xét tam giác AIB và tam giác DIC có AB // CD ( ABCD là hình thang )

\(\frac{AI}{IC}=\frac{IB}{ID}=\frac{AB}{DC}\)

mà \(\frac{BE}{AC}=\frac{AB}{DC}=\frac{IB}{ID}\Rightarrow BE.DC=AB.AC\)

a: Xét ΔBDC vuông tại B và ΔHBC vuông tại H có

góc C chung

=>ΔBDC đồng dạng vói ΔHBC

b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)

HC=15^2/25=9cm

HD=25-9=16cm

Áp dụng các hệ thức lượng trong tam giác vuông BDC cùng chú ý độ dài đường cao hạ từ B xuống CD bằng AD, ta tính được : AB = 9cm, BD =15cm, hoặc AB = 16cm, BC = 15cm, BD = 20cm

a: Xét tứ giác ABFD có

AB//FD

BF//AD

=>ABFD là hình bình hành

=>AB=DF

Xét tứ giác ABCK có

AB//CK

AK//BC

=>ABCK là hình bình hành

=>AB=CK=DF

c: Xet ΔMAB và ΔMKD có

góc MAB=góc MKD

góc AMB=góc KMD

=>ΔMAB đồng dạng với ΔMKD

=>MB/MD=AB/KD

BP/PC=DF/FC

mà KD=FC

và AB=DF

nên MB/MD=BP/PC

=>MP//DC

Kẻ thêm đường cao BH xuống DC \(\left(H\in DC\right)\)

Dễ thấy \(ABHD\) là hcn nên \(AD=BH=10\left(cm\right)\)

Áp dụng HTL cho ...

\(BH^2=DH\cdot HC\Rightarrow HD\cdot HC=100\)

Mà \(HD+HC=CD=20\left(cm\right)\)

\(\Rightarrow\left\{{}\begin{matrix}HD\cdot HC=100\\HD+HC=20\end{matrix}\right.\Rightarrow HD=HC=10\)

Ta có \(BD=\sqrt{HD^2+HB^2}=\sqrt{10^2+10^2}=10\sqrt{2}\left(cm\right)\left(pytago\right)\)

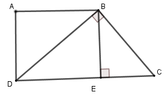
Kẻ BE ⊥ CD tại E

Suy ra tứ giác ABED là hình chữ nhật (vì A ^ = D ^ = E ^ = 90 ∘ ) nên BE = AD = 12cm

Đặt EC = x (0 < x < 20) thì DE = 20 – x

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông BCD ta có:

B E 2 = E D . E C ⇔ x(20 – x) = 100 ⇔ x 2 - 20 X + 100 = 0

⇔ ( x - 10 ) 2 = 0 ⇔ x = 10 (tm)

Với EC = 10, theo định lý Pytago ta có BC =  B E 2 + E C 2 = 10 2 + 10 2 = 10 2

Vậy BC = 10 2 cm

Đáp án cần chọn là: B

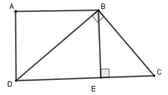
Kẻ BE ⊥ CD tại E

Suy ra tứ giác ABED là hình chữ nhật (vì A ^ = D ^ = E ^ = 90 ∘ ) nên BE = AD = 12cm

Đặt EC = x (0 < x < 25) thì DE = 25 – x

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông BCD ta có:

B E 2 = E D . E C ⇔ x ( 25 - x ) = 144 ⇔ x 2 - 25 x + 144 = 0

  x 2 - 16 x - 9 x + 144 = 0 <=> x(x – 16) – 9(x – 16) = 0 <=> (x – 16)(x – 9) = 0

⇔ x = 16 x = 9 (thỏa mãn)

Với EC = 16, theo định lý Pytago ta có BC = B E 2 + E C 2 = 12 2 + 16 2 = 20  (loại)

Với EC = 9, theo định lý Pytago ta có BC = B E 2 + E C 2 = 12 2 + 9 2 = 15  (nhận)

Vậy BC = 15cm

Đáp án cần chọn là: A