Cho hình chữ nhật ABCD , từ A kẻ AH vuông góc với BD .
a, Chứng minh \(BC^2=DH.DB\)
b, Gọi S là trung điểm BH , R là trung điểm AH .
Chứng tỏ : SH.BD=SR.DC
c, Gọi I là trung điểm DC . Chứng tỏ tứ giác DRST là hình bình hành .
Những câu hỏi liên quan
Cho hình chữ nhật ABCD , từ A kẻ AH vuông góc với BD .
a, Chứng minh \(BC^2\)=DH.DB
b, Gọi S là trung điểm BH , R là trung điểm AH .
Chứng tỏ : SH.BD=SR.DC
c, Gọi I là trung điểm DC . Chứng tỏ tứ giác DRST là hình bình hành
Cho hình chữ nhật ABCD, kẻ AH vuông góc với đường chéo BDa) Chứng minh ΔAHD và ΔDCB đồng dạng và
B
C
2
D
H
.
D
B
b) Gọi S là trung điểm của BH, R là trung điểm của AH.Chứng minh SH.BD SR.DCc) Gọi T là trung điểm của DC. Chứng minh tứ giác DRST là hình bình hànhd) Tính góc AST
Đọc tiếp
Cho hình chữ nhật ABCD, kẻ AH vuông góc với đường chéo BD
a) Chứng minh ΔAHD và ΔDCB đồng dạng và B C 2 = D H . D B
b) Gọi S là trung điểm của BH, R là trung điểm của AH.
Chứng minh SH.BD = SR.DC
c) Gọi T là trung điểm của DC. Chứng minh tứ giác DRST là hình bình hành
d) Tính góc AST
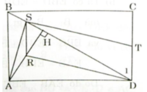
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
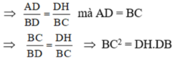
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
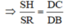
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o
Đúng 1
Bình luận (0)
giúp mình gấp nha!!!
cho hình chữ nhật ABCD kẻ AH vuông góc với đường chéo BD
a) chứng minh tam giác AHD và tam giác DCB đồng dạng và BC^2 = với DH.DB
b) gọi S là trung điểm của BH , R là trung điểm của AH ,chứng minh SH.BD=SR.DC
C) Gọi T là trung điểm DC, chứng minh tứ giác DRST là hình bình hành
D) tính góc AST
Cho hcn ABCD, kẻ AH vuông góc với đường chéo BD.
a. Chứng minh BC2=DH.DB.
b. Gọi S là trung điểm của BH, R là trung điểm của AH. Chứng minh SH.BD=SR.DC.
c.Gọi T là trung điểm của DC. Chứng minh tứ giác DRST là hình bình hành.
d. Tính số đo góc AST.
Cho hình chữ nhật ABCD.Từ A kẻ AH vuông góc với đường chéo BD.
a/ Chứng minh AHD ~ BDC
b/ Gọi S là trung điểm của BH, R là trung điểm của AH.Chứng minh SH.BD = SR.DC
c/ biet AB =4cm AD = 3cm. Tinh do dai doan SH
Mong mn giúp mk làm phần in đậm , mk cần gấp ạ. Xin cảm ơn!!!Bài 1 Cho tam giác ABC, trung tuyến AD, biết AB 4cm, AC 8cm. Qua B dựng đường thắng cắt AC tại F sao cho góc ABF bằng góc ACB. a) Chứng tỏ tam giác ABF và tam giác ACB đồng dạng. Tính độ dài đoạn CFb) Chứng tỏ diện tích tam giác ABC bằng hai lần diện tích tam giác ADCc) Gọi 0 là giao điểm của BF và AD, CO cắt AB tại E. Từ A và C lần lượt dựng các đường | thẳng song song với BF cắt CO tại J và cắt AD tại I. + Chứng tỏ FC/FA CI/JA +...
Đọc tiếp
Mong mn giúp mk làm phần in đậm , mk cần gấp ạ. Xin cảm ơn!!!
Bài 1 Cho tam giác ABC, trung tuyến AD, biết AB = 4cm, AC = 8cm. Qua B dựng đường thắng cắt AC tại F sao cho góc ABF bằng góc ACB.
a) Chứng tỏ tam giác ABF và tam giác ACB đồng dạng. Tính độ dài đoạn CF
b) Chứng tỏ diện tích tam giác ABC bằng hai lần diện tích tam giác ADC
c) Gọi 0 là giao điểm của BF và AD, CO cắt AB tại E. Từ A và C lần lượt dựng các đường | thẳng song song với BF cắt CO tại J và cắt AD tại I.
+ Chứng tỏ FC/FA = CI/JA
+ Chứng tỏ DB/DC = FC/FA = EA/EB=1
Bài 2: Cho hình chữ nhật ABCD, kẻ AH vuông góc với đường chéo BD
a) Chứng minh tam giác AHD và tam giác DCB đồng dạng và BC.BC = DH.DB
b) Gọi S là trung điểm của BH, R là trung điểm của AH.
Chứng minh SH.BD = SR.DC
c) Gọi T là trung điểm của DC. Chứng minh tứ giác DRST là hình bình hành
d) Tính góc AST
câu 2d
Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o
...
Chúc bạn học tốt
câu 1d
+ ΔACI có BF//CI→ FC/FA=OI/AO
IΔCOI có AJ//CI (//BF)→ CI/AJ=OI/AO
→FC/FA=CI/AJ
Cho hình chữ nhật ABCD . Kẻ BH vuông góc với AC tại H , M là trung điểm của AH . Kẻ ME vuông góc với DC tại E, MF vuông góc với BC tại F
a) Chứng minh MC= EF
b) MF cắt BH ở I . Chứng minh CI vuông góc với MB
c) Gọi K là trung điểm của DC Chứng minh MICK là hình bình hành
d) Chứng minh BMI = EMK
a: Xét tứ giác MFCE có
\(\widehat{MFC}=\widehat{MEC}=\widehat{FCE}=90^0\)
Do đó: MFCE là hình bình hành
Suy ra: MC=EF
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Gọi M và N theo thứ tự là đường trung điểm của AH và DH.
a, Chứng minh MN // AD
b, gọi I là trung điểm của BC chứng minh góc BMNI là hình bình hành
a: Xét ΔAHD có
M là trung điểm của HA
N là trung điểm của HD
Do đó: MN là đường trung bình của ΔAHD
Suy ra: MN//AD
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD từ A kẻ AH vuông góc với BD
a) C/minh AHD đồng dạng với BCD
b) Gọi S là trung điểm của BH, R là trung điểmcủa AH. C/minh SH.BD = SR.DC
c) Biết AB = 4 , AD = 3. Tính SB?
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó:ΔAHB\(\sim\)ΔBCD
b: Xét ΔHAB có
R là trung điểm của HA
S là trung điểm của HB
Do đo: RS là đường trung bình
=>RS//AB
Xét ΔHSR vuông tại H và ΔCDB vuông tại C có
\(\widehat{HSR}=\widehat{CDB}\)
Do đó: ΔHSR\(\sim\)ΔCDB
Suy ra: SH/DC=SR/DB
hay \(SH\cdot BD=SR\cdot DC\)
Đúng 0
Bình luận (0)