PTĐTTNT:
xn + xn+3 -xn
Những câu hỏi liên quan
cho dãy (xn) thỏa mãn x1=1
xn+1 - căn(xn+1) = xn + căn(xn) + 1/(n+4)
tính lim(xn/(n2))
Cho dãy (xn) thỏa 1<xn<2 và xn+1=1+xn-1/2xn^2 với mọi n thuộc N
a,chứng minh |xn-căn 2|<(1/2)^n với mọi n lớn hơn hoặc bằng 3
b,Tính lim xn
Bài 4: Làm tính nhân
a) xn. yn+2.(xy+x2y+1)
b) (4xn-2+xn+1).xn
c) 4xy.(xn-2 yn+1+ xn yn+1)
tim cac so x1,x2,...,xn-1 ,xn biet rang x1/a1=x2/a2=...=xn/an va x1+x2+...+xn=c
vao thong tin tai khoan o cho hinh tam giac ben canh ten cua ban roi an vao doi anh hien thi .xong
Đúng 0
Bình luận (0)
Phân tích đa thức sau thành nhân tử : xn + 3 + xn
\(x^{n+3}+x^n=x^n.x^3+x^n=x^n\left(x^3+1\right)=x^n\left(x+1\right)\left(x^2-x+1\right)\)
Đúng 2
Bình luận (0)
\(x^{n+3}+x^n=x^n\left(x^3+1\right)=x^n\left(x+1\right)\left(x^2-x+1\right)\)
Đúng 0
Bình luận (0)
\(x^{n+3}+x^n=x^n\left(x^3+1\right)=x^n\cdot\left(x+1\right)\left(x^2-x+1\right)\)
Đúng 0
Bình luận (0)
Cho dãy số
(
x
n
)
:
x
0
1
x
n
2
n
(...
Đọc tiếp
Cho dãy số ( x n ) : x 0 = 1 x n = 2 n ( n - 1 ) 2 ∑ i = 1 n - 1 x i , n = 2 , 3 . . . . . Xét dãy số yn = xn+1 - xn. Khẳng định nào đúng về dãy (yn)
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn A.
Ta có: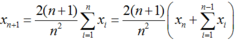 
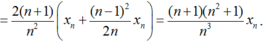
Do đó: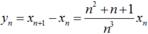 
- Ta chứng minh dãy (yn) tăng.
Ta có: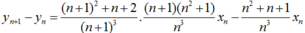 
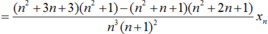
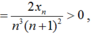
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
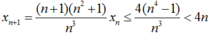
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: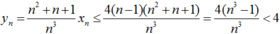 
Vậy bài toán được chứng minh.
Đúng 0
Bình luận (0)
Xét hàm số
f
x
2
x
2
-
2
x
x
-
1
1. Cho biến x những giá trị khác 1 lập thành dãy số
x
n
,
x
n...
Đọc tiếp
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:
Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).
Rút gọn biểu thức
x
n
(
x
n
+
1
+
y
n
)
-
y
n
(
x
n
+
y
n
-
1
)
được kết quả là? A.
x
2
n
+...
Đọc tiếp
Rút gọn biểu thức x n ( x n + 1 + y n ) - y n ( x n + y n - 1 ) được kết quả là?
A. x 2 n + 1 - y 2 n - 1
B. x 2 n - y 2 n
C. x 2 n - 1 - y 2 n + 1
D. x n + 1 - y n - 1
Cho a>1 và dãy số (xn) xác định như sau:
x1=a; xn+1= \(\sqrt{a.x_n^2+3x_n+4}\) với n=1,2,...
a. Tìm limxn.
b. Tìm a đề xn+1/xn =4.
Đề bài sai, dãy tăng và không hề bị chặn trên nên không tồn tại giới hạn
Đúng 0
Bình luận (0)
cho dãy un xác định x1=0, x2=1 và xn+2= xn +1/(xn+1+xn+2)
chứng minh dãy un có giới hạn hữu hạn và tính giời hạn đó
\(u_n:\left\{{}\begin{matrix}u_1=0;u_1=1\\u_{n+2}=\dfrac{u_{n+1}}{u_{n+1}+u_{n+2}}\end{matrix}\right.\)
Giả sử \(limu_n=a\Rightarrow limu_{n+1}=limu_{n+2}=a\)
\(\Rightarrow a=\dfrac{a}{a+a}=\dfrac{a}{2a}=\dfrac{1}{2}\)
Nên dãy \(u_n\) có giới hạn hữu hạn
vì \(\left\{{}\begin{matrix}u_1=0\\u_2=1>0\end{matrix}\right.\)
\(\Rightarrow u_{n+2}=\dfrac{u_{n+1}}{u_{n+1}+u_{n+2}}>0,\forall n\inℕ\)
\(\Rightarrow a>0\)
\(\Rightarrow limu_n=a=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)