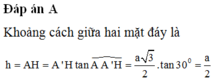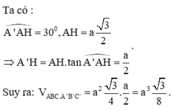cho lăng trụ ABC.A'B'C' có tất cả các cạnh đáy đều bằng a, góc tạo bởi cạnh bên và mặt đáy là 60 độ và hình chiếu H của đỉnh A lên mp (A'B'C') trùng với trung điểm của cạnh B'C'.

Những câu hỏi liên quan
cho lăng trụ ABC.A'B'C' có tất cả các cạnh đáy đều bằng a, góc tạo bởi cạnh bên và mặt đáy là 60 độ và hình chiếu H của đỉnh A lên mp (A'B'C') trùng với trung điểm của cạnh B'C'.
Cho lăng trụ ABC.ABC có tất cả các cạnh đáy bằng a. Biết góc tạo bởi cạnh bên và mặt đáy là
60
o
và H là hình chiếu của đỉnh A lên mặt phẳng (ABC) , H trùng với trung điểm của cạnh BC. Góc giữa BC và AC là
α
. Giá trị của
tan
α
là? A. 3 B. -3 C.
1
3
D....
Đọc tiếp
Cho lăng trụ ABC.A'B'C' có tất cả các cạnh đáy bằng a. Biết góc tạo bởi cạnh bên và mặt đáy là 60 o và H là hình chiếu của đỉnh A lên mặt phẳng (A'B'C') , H trùng với trung điểm của cạnh B'C'. Góc giữa BC và AC' là α . Giá trị của tan α là?
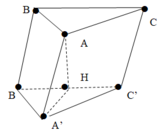
A. 3
B. -3
C. 1 3
D. - 1 3
Đáp án A
Hướng dẫn giải:
Ta có A'H là hình chiếu của AA' lên mặt phẳng đáy
Do đó
![]()
Lại có A ' H = a 2
⇒ A H = tan 60 o . a 2 = a 3 2 = B ' H
nên A ' B = a 6 2
Và A A ' = A ' H cos 60 o = a ⇒ A C ' = a
Mặt khác
![]()
Do đó cos α = A C ' 2 + B ' C ' 2 - A B ' 2 2 . A C ' . B ' C ' = 1 4
Suy ra tan α = 1 cos 2 α - 1 = 3
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác ABC.A'B'C' có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc \(60^0\) và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A'B'C') trùng với trung điểm của cạnh B'C'
a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ
b) Chứng minh rằng mặt bên BCC'B' là một hình vuông
Cho hình lăng trụ tam giác ABC.ABCcó tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc
60
ο
và hình chiếu vuông góc của đỉnh A lên mặt phẳng (ABC) trùng với trung điểm của cạnh BC.a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ.b) Chứng minh rằng mặt bên BCCB là một hình vuông.
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A'B'C'có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc 60 ο và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A'B'C') trùng với trung điểm của cạnh B'C'.
a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ.
b) Chứng minh rằng mặt bên BCC'B' là một hình vuông.
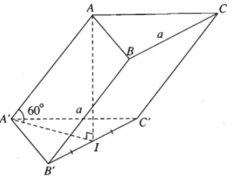
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
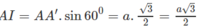
b) 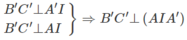
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.
Đúng 0
Bình luận (0)
cho lăng trụ tam giác ABCA'B'C' có tất cả các cạnh bên bằng nhau và bằng a. biết góc tạo bởi cạnh bên và mặt đáy bằng 60 độ. hình chiếu của A lên (A'B'C') trùng với trung điểm của B'C. tính tan góc giữa (ABB'A') và mặt đáy
(giúp em với ạ)
Cho hình lăng trụ ABC.ABC có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng
30
0
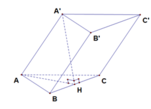
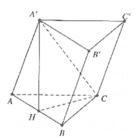
. Hình chiếu H của A trên mặt phẳng (ABC) là trung điểm của B’C’. Tính theo a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.ABC.
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30 0 . Hình chiếu H của A trên mặt phẳng (A'B'C') là trung điểm của B’C’. Tính theo a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.A'B'C'.
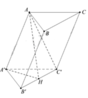
![]()
![]()

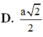
Cho hình lăng trụ
A
B
C
.
A
B
C
có đáy là tam giác đều cạnh a, góc giữa cạnh bên và mặt phẳng đáy bằng
30
°
. Hình chiếu của đỉnh A trên mp(ABC) trùng với trung điểm của cạnh BC.Tính thể tích của khối lăng trụ đã cho. A.
a
3
3
8
B.
a...
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có đáy là tam giác đều cạnh a, góc giữa cạnh bên và mặt phẳng đáy bằng 30 ° . Hình chiếu của đỉnh A' trên mp(ABC) trùng với trung điểm của cạnh BC.Tính thể tích của khối lăng trụ đã cho.
A. a 3 3 8
B. a 3 3 3
C. a 3 3 12
D. a 3 3 4
Cho hình lăng trụ ABC.ABC có mặt đáy ABC là tam giác đều, độ dài cạnh AB 2a. Hình chiếu vuông góc của A lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng
60
°
, tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACCA) A.
h
39
a
13
B.
h
2
15...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều, độ dài cạnh AB = 2a. Hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 60 ° , tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')
A. h = 39 a 13
B. h = 2 15 a 5
C. h = 2 21 a 7
D. h = 15 a 5
Đáp án B.
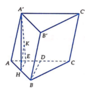
Do H là trung điểm AB nên d B ; A C C ' A ' d H ; A C C ' A ' = B A H A = 2
⇒ d B ; A C C ' A ' = 2 d d H ; A C C ' A '
Ta có A H ' ⊥ A B C nên A A ' , ( A B C ) ⏜ = A ' A , H A ⏜ = A ' A H ⏜ = 60 °
Gọi D là trung điểm của AC thì B D ⊥ A C .
Kẻ H E ⊥ A C , E ∈ A C → H E / / B D
Ta có A C ⊥ A ' H A C ⊥ H E ⇒ A C ⊥ A ' H E ⊥ A C C ' A '
Trong A ' H E kẻ H K ⊥ A ' E , K ∈ A ' E ⇒ H K ⊥ A C C ' A '
Suy ra
d H ; A C C ' A ' = H K ⇒ 2 d B ; A C C ' A ' = 2 H K
Ta có B D = 2 a 3 2 = a 3 ⇒ H E = 1 2 B D = a 3 2
Xét tam giác vuông A ' A H có A H ' = A H . tan 60 ° = a 3
Xét tam giác vuông A ' H E có 1 H K 2 = 1 A ' H 2 + 1 H E 2 = 1 a 3 2 + 1 a 3 2 2 = 5 3 a 2 ⇒ H K = a 15 5 .
Vậy d B ; A C C ' A ' = 2 H K = 2 a 15 5
Đúng 0
Bình luận (0)
Cho hình lăng trụ
A
B
C
.
A
B
C
có mặt đáy là tam giác đều cạnh
A
B
2
a
. Hình chiếu vuông góc của A lên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng
60
°
. Góc giữa đường thẳng AC và (ABC) là A.
π
4
B.
π...
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có mặt đáy là tam giác đều cạnh A B = 2 a . Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 60 ° . Góc giữa đường thẳng A'C và (ABC) là
A. π 4
B. π 3
C. a r c sin 1 4
D. π 6
Cho lăng trụ (ABC ABC) có tất cả các cạnh đều bằng a Góc tạo bởi cạnh bên và mặt đáy bằng
30
°
. Hình chiếu H của điểm A lên mặt phẳng (ABC) thuộc đường thẳng BC. Tính khoảng cách từ điểm B đến mặt phẳng (ACCA) A.
a
3
4
B.
a
21
14
C.
a
21...
Đọc tiếp
Cho lăng trụ (ABC A'B'C') có tất cả các cạnh đều bằng a Góc tạo bởi cạnh bên và mặt đáy bằng 30 ° . Hình chiếu H của điểm A lên mặt phẳng (ABC) thuộc đường thẳng BC. Tính khoảng cách từ điểm B đến mặt phẳng (ACC'A')
A. a 3 4
B. a 21 14
C. a 21 7
D. a 3 2
Đáp án C
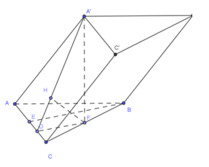
Gọi F là hình chiếu của A' lên mp (ABC), Nên góc A ' A F ^ là góc tạo bởi cạnh bên của AA' với (ABC), ⇒ A ' A F ^ = 30 0 ⇒ A F = A A ' cos 30 0 = 3 2 a ⇒
F là trung điểm của BC , gọi D,E là hình chiếu của F, B lên AC,H là hình chiếu của F lên AD. Dễ dàng chứng minh được FH là hình chiếu của F trên (ACC'A'), Ta có
d B , A C C ' A ' = 2 d F , A C C ' A ' = 2 F H .
A ' F = A A ' . c o s 30 0 = 1 2 a ; F D = 1 2 B E = 3 4 a
1 F H 2 = 1 A F 2 + 1 F D 2 ⇒ F H = a 21 7
Đúng 0
Bình luận (0)