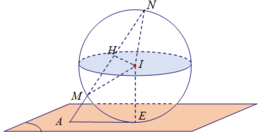
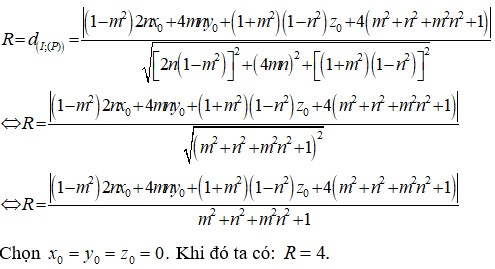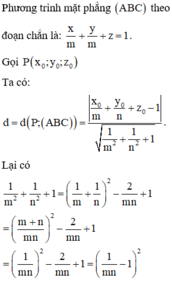Trong không gian với hệ tọa độ OXYZ cho pt mặt phẳng (P) : \((1-m^2).2nx+4mny+(1+m^2)(1-n^2)z+4(m^2.n^2+m^2+n^2+1)=0\) với m,n là tham số thực tùy ý. biết mp(P) luôn tiếp xúc với 1 mặt cầu cố định . tìm bán kính của mặt cầu đó.

Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình
1
-
m
2
2
n
.
x
+
4
m
n
.
y
+
1
+
m
2
1
-
n...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình 1 - m 2 2 n . x + 4 m n . y + 1 + m 2 1 - n 2 . z + 4 m 2 n 2 + m 2 + n 2 + 1 = 0 , với m, n là tham số thực tùy ý. Biết rằng mặt phẳng (P) luôn tiếp xúc với một mặt cầu cố định khi m, n thay đổi. Tìm bán kính mặt cầu đó?
A. 1
B. 2
C. 3
D. 4
Đáp án D.
Gọi I(a,b,c) là tâm mặt cầu cố định đó. Rõ ràng d(I,(P)) = R không đối với mọi m , n ∈ ℝ .
Với m = 1 ⇒ d I , P = 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
Với m = - 1 ⇒ d I , P = - 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
⇒ 2 n b + 1 - n 2 c + 4 n 2 + 1 = - 2 n b + 1 - n 2 c + 4 n 2 + 1 ⇔ [ b = 0 1 - n 2 c + 4 n 2 + 1 = 0
Rõ ràng 1 - n 2 c + 4 n 2 + 1 = 0 không thể xảy ra với mọi n ∈ ℝ suy ra b = 0
Với m = n = 1 ⇒ d I , P = b + 4 = R = 4 .
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;0;2) ; N(1;-1;-1) và mặt phẳng (P): x + 2y - z + 2 0. Một mặt cầu đi qua M ; N tiếp xúc với mặt phẳng (P) tại điểm E . Biết E luôn thuộc một đường tròn cố định, tính bán kính đường tròn đó.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;0;2) ; N(1;-1;-1) và mặt phẳng (P): x + 2y - z + 2 = 0. Một mặt cầu đi qua M ; N tiếp xúc với mặt phẳng (P) tại điểm E . Biết E luôn thuộc một đường tròn cố định, tính bán kính đường tròn đó.
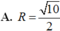
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
(
P
)
:
(
1
-
m
2
)
2
n
x
+
4
m
n
y
+
(
1
+
m
2
)
(
1
-
n
2
)
z
+
4
(
m...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : ( 1 - m 2 ) 2 n x + 4 m n y + ( 1 + m 2 ) ( 1 - n 2 ) z + 4 ( m 2 + n 2 + m 2 n 2 + 1 ) = 0 Biết (P) luôn tiếp xúc với mặt cầu cố định. Khi đó bán kính mặt cầu cố định đó là:
A. 1
B. 2
C. 3
D. 4
Trong không gian hệ trục tọa độ Oxyz, cho mặt phẳng
P
:
1
−
m
2
2
n
x
+
4
m
n
y
+
1
+
m
2
1
−
n
2...
Đọc tiếp
Trong không gian hệ trục tọa độ Oxyz, cho mặt phẳng P : 1 − m 2 2 n x + 4 m n y + 1 + m 2 1 − n 2 z + 4 m 2 + n 2 + m 2 n 2 + 1 = 0 . Biết (P) luôn tiếp xúc với mặt cầu cố định. Khi đó bán kính mặt cầu cố định đó là
A. 1
B. 2
C. 3
D. 4
Đáp án D
Hướng giải: Ta sẽ đi tìm 1 mặt phẳng song song với (P), đồng thời tiếp xúc với mặt cầu. Lúc này, khoảng cách giữa 2 mặt phẳng này chính là 2 lần bán kính mặt cầu.
Do (P) luôn tiếp xúc với 1 mặt cầu cố định => Ta chọn tùy ý m, n để được 2 mặt phẳng song song
+ Chọn m=1,n=1 =>4y+16=0 => y = - 4 ( α 1 )
+ Chọn m=-1,n=1 => -4y+16=0 => y=4 ( α 2 )
d ( ( α 1 ) , ( α 2 ) ) = 8 = > r = 4
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, xét các điểm
A
0
;
0
;
1
,
B
m
;
0
;
0
,
C
0
;
n
;
0
,
D...
Đọc tiếp
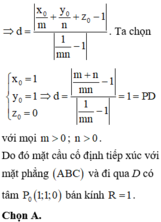
Trong không gian với hệ tọa độ Oxyz, xét các điểm A 0 ; 0 ; 1 , B m ; 0 ; 0 , C 0 ; n ; 0 , D 1 ; 1 ; 1 với m > 0, n > 0 và m + n = 1 . Biết rằng khi m, n thay đổi, tồn tại một mặt cầu cố định tiếp xúc với mặt phẳng (ABC) và đi qua D. Tính bán kính R của mặt cầu đó.
A. R = 1
B. R = 2 2
C. R = 3 2
D. R = 3 2
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
2
2
y
-
1
z
4
và mặt cầu (S):
(
x
-
1
)
2
+
(
y
-
2
)
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 2 2 = y - 1 = z 4 và mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 1 ) 2 = 2. Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với (S). Gọi M,N là tiếp điểm. Tính độ dài đoạn thẳng MN.
A. 2 2
B. 4 3
C. 6
D. 4
1 cho số phức za+bi (b0) thỏa z+overline{z} 10 và /z/ 13. giá trị của a+b là
2 pt z^2+ax+b0,(a,bin R) có một nghiệm z-2+i .giá trị của a-b la
3 gọi z1,z2 là hai nghiệm phức của pt z^2+2z+80, trong đó z1 có phần ảo dương . số phức w(2z1+z2).overline{z}_1 là
4 kí hiệu z1,z2, z3 va z4 là bốn nghiệm phức của pt z^4-z^2-120. giá trị của T/z1/+/z2/+/z3/+/z4/ bằng
5 trong ko gian hệ tọa độ oxyz, cho 2 điểm M(3;-2;1),N(0;1;-1). tìm độ dài của đoạn thẳng
6 trong ko gian với tọa độ oxyz. cho 2 điể...
Đọc tiếp
1 cho số phức z=a+bi (b>0) thỏa z+\(\overline{z}\) =10 và /z/ =13. giá trị của a+b là
2 pt z^2+ax+b=0,(a,b\(\in\) R) có một nghiệm z=-2+i .giá trị của a-b la
3 gọi z1,z2 là hai nghiệm phức của pt z^2+2z+8=0, trong đó z1 có phần ảo dương . số phức w=(2z1+z2).\(\overline{z}_1\) là
4 kí hiệu z1,z2, z3 va z4 là bốn nghiệm phức của pt z^4-z^2-12=0. giá trị của T=/z1/+/z2/+/z3/+/z4/ bằng
5 trong ko gian hệ tọa độ oxyz, cho 2 điểm M(3;-2;1),N(0;1;-1). tìm độ dài của đoạn thẳng
6 trong ko gian với tọa độ oxyz. cho 2 điểm A(-3;1;-4 va B(1;-1;2). pt mặt cầu S nhận AB làm đường kính là
7 trong ko gian vói hệ tọa độ oxyz, viết pt mặt cầu tâm I(3;2;4) và tiếp xúc với trục oy là
8 pt mặt cầu S tâm I(1;3;5) và tiếp cú với đường thẳng \(\frac{x}{1}=\frac{y+1}{-1}=\frac{z-2}{-1}\) là
9 trong không gian với hệ tọa độ oxyz , cho điểm I(-1;0;0) và đường thẳng d:\(\left\{{}\begin{matrix}x=2+t\\y=1+2t\\z=1+t\end{matrix}\right.\) pt mặt cầu S có tâm I và tiếp xúc với đường thẳng d là
10 trong ko gian với hệ tọa độ oxyz, cho 2 điểm A(1;2;2),B(3;-2-0). viết pt mặt phẳng trung trực đoạn AB
11 trong ko gian với hệ tọa độ oxyz, cho 2 điểm A(4;0;1) và B(-2;2;3). pt mặt phẳng trung trực đoạn AB là
12 trong ko gian oxyz, mặt phẳng \(\alpha\) đi qua gốc tọa độ(0;0;0) va2 co1 vecto phap tuyen n=(6;3;-2) thi co pt ?
13 trong ko gian oxyz , cho 2 điểm A(1;-2;4) B(2;1;2). viết pt mặt phẳng (P) vuông góc với đường AB tại điểm A LÀ
14 Trong ko gian với hệ tọa độ oxyz ,mp qua A(2;3;1) và B(0;1;2).pt mặt phẳng (P) đi qua A và vuông góc AB là
15 trong ko gian hệ tọa độ oxyz, ,p đi qua điểm A (2;-3;-2) và có vecto pháp tuyến \(\overline{n}\)=(2;-5;1) có pt là
16 viết pt mặt phẳng (P) qua A (1;1;1) vuông góc với hai mp \(\alpha\) :x+y-z-2=0 \(\beta\) x-y+z-1=0
17 trong ko gian với hệ tọa độ oxyz cho hai mp(p):x-y+z=0,(Q):3x+2y-12z+5=0 , viết pt mặt phẳng (R) đi qua O và vuông góc với (P),(Q)
18 trong ko gian hệ tạo độ oxyz, mp(Q) đi qua 3 điểm ko thẳng hang M(2;2;0),N(2;0;3),P(0;3;3) có pt là
19 trong ko gian với hệ tọa độ oxyz cho mặt phẳng \(\alpha\) cắt 3 trục tọa M (3;0;0),N(0;-4;0) ,P(0;0;-2). pt mặt phẳng \(\alpha\)?
20 rong ko gian với hệ tọa độ oxyz , cho ba điểm A(1;0;0),B(0;2;0)C(0;0;3). HỎI MẶT MẶT PHẲNG NÀO DƯỚI ĐÂY ĐI QUA BA ĐIỂM A,B VÀ C
A (q) X/3+Y/2+Z/3=1 B (S)X+2Y+3Z=-1
C (P) X/1+Y/2+Z/3=0 D (r):X+2Y+3Z=1
1.
\(\left\{{}\begin{matrix}a+bi+a-bi=10\\\sqrt{a^2+b^2}=13\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2a=10\\a^2+b^2=169\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=5\\b=12\end{matrix}\right.\)
2.
\(\left(-2+i\right)^2+a\left(-2+i\right)+b=0\)
\(\Leftrightarrow3-4i-2a+ai+b=0\)
\(\Leftrightarrow\left(-2a+b+3\right)+\left(a-4\right)i=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2a+b+3=0\\a-4=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=4\\b=5\end{matrix}\right.\)
3.
\(z^2+2z+8=0\Rightarrow\left[{}\begin{matrix}z_1=-1+7i\\z_2=-1-7i\end{matrix}\right.\)
\(\Rightarrow w=10+2\sqrt{7}i\)
Đúng 0
Bình luận (0)
4.
\(z^4-z^2-12=0\Rightarrow\left[{}\begin{matrix}z=4\\z=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}z=2\\z=-2\\z=i\sqrt{3}\\z=-i\sqrt{3}\end{matrix}\right.\) \(\Rightarrow T=4+2\sqrt{3}\)
5.
\(\overrightarrow{NM}=\left(3;-3;2\right)\Rightarrow MN=\sqrt{3^2+3^2+2^2}=\sqrt{22}\)
6.
\(\overrightarrow{AB}=\left(4;-2;6\right)\Rightarrow R=\frac{AB}{2}=\frac{1}{2}\sqrt{4^2+2^2+6^2}=\sqrt{14}\)
Gọi I là trung điểm AB \(\Rightarrow I\left(-1;0;-1\right)\)
Pt mặt cầu:
\(\left(x+1\right)^2+y^2+\left(z+1\right)^2=14\)
Đúng 0
Bình luận (0)
7.
\(R=d\left(I;Oy\right)=\sqrt{x_I^2+z_I^2}=5\)
Pt mặt cầu:
\(\left(x-3\right)^2+\left(y-2\right)^2+\left(z-4\right)^2=25\)
8.
Đường thẳng d qua điểm \(M\left(0;-1;2\right)\) và nhận \(\overrightarrow{u}=\left(1;-1;-1\right)\) là 1 vtcp
\(\overrightarrow{MI}=\left(1;4;3\right)\)
\(\Rightarrow R=d\left(I;d\right)=\frac{\left|\left[\overrightarrow{u};\overrightarrow{MI}\right]\right|}{\left|\overrightarrow{u}\right|}=\frac{\left|\left(-1;4-;5\right)\right|}{\left|\left(1;-1;-1\right)\right|}=\sqrt{14}\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=14\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng
d
:
x
-
2
2
y
-
1
z
4
và mặt cầu (S): (x-1)2+ (y-2)2 + (z-1)22. Hai mặt phẳng (P), (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d : x - 2 2 = y - 1 = z 4 và mặt cầu (S): (x-1)2+ (y-2)2 + (z-1)2=2. Hai mặt phẳng (P), (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
(
P
)
:
x
+
y
–
z
–
4
0
và điểm M (1;–2;-2). Tọa độ điểm N đối xứng với điểm M qua mặt phẳng (P) là A. N (3;4;8) B. N (3;0;–4) C. N (3;0;8) D. N (3;4;–4)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : x + y – z – 4 = 0 và điểm M (1;–2;-2). Tọa độ điểm N đối xứng với điểm M qua mặt phẳng (P) là
A. N (3;4;8)
B. N (3;0;–4)
C. N (3;0;8)
D. N (3;4;–4)