đây bạn nhé

BC=2cm

AD²=8²+6²= 100 = 10cm

AB²=10²+2²= Xấp xỉ của 10cm

CD²=4²+4²= 32 = xấp xỉ của 6cm

Xét ∆AHB và ∆ CKD có:HB = KD (= 1 ô)AHBˆ = CKDˆAH = CK (= 3 ô)=> ∆AHB = ∆CKD(c.g.c)=> AB = CD (cạnh tương ứng)Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)suy ra BC=AD.b) Xét ∆ABD và ∆CDB có:AB = CD (cmt)BC = AD (cmt)BD chung.=> ∆ABD = ∆CDB (c.c .c)=> ABDˆ = CDBˆMà hai góc này ở vị trí so le trongVậy AB // CD (đpcm)

chả bt có khớp ko chứ lười đọc quá

x

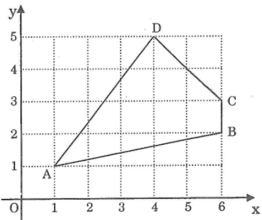
Ta có hình vẽ:

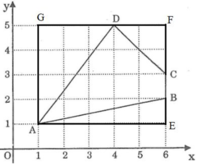
+) Áp dụng định lí py –ta-go vào tam giác ABE vuông tại E ta có:

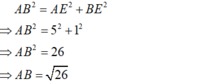
+) Áp dụng định lí py – ta- go vào tam giác DFC vuông tại F có:

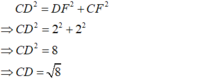
+) Áp dụng định lí Py-ta-go vào tam giác AGD vuông tại G ta có:

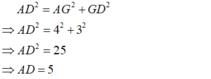
+) BC = 1

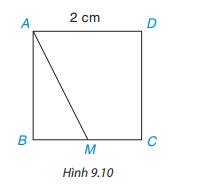
a) Đường vuông góc kẻ từ A đến BC là: AB

Đường xiên kẻ từ A đến BC là: AM

b) AB < AM (Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.)

c) Vì CB \( \bot \) AB nên khoảng cách từ C đến AB là độ dài CB =  2 cm

zồi ôi dài quá

Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)

nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất tia phân giác của tam giác)

hay \(\dfrac{BD}{4}=\dfrac{CD}{6}\)

mà BD+CD=BC=4cm(D nằm giữa B và C)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BD}{4}=\dfrac{CD}{6}=\dfrac{BD+CD}{4+6}=\dfrac{4}{10}=\dfrac{2}{5}\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{BD}{4}=\dfrac{2}{5}\\\dfrac{CD}{6}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=\dfrac{8}{5}cm\\CD=\dfrac{12}{5}cm\end{matrix}\right.\)

Vậy: \(BD=\dfrac{8}{5}cm;CD=\dfrac{12}{5}cm\)