Tìm h/s: y = \(ax^2+bx+c\) biết rằng hàm số đạt giá trị cực đại = 3 tại x= 2 và đồ thị đi qua A(0;-1)
Giúp em vs nha các acj
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; −1). Tính tổng S = a + b + c.
A. S = -1
B. S = 4
C. S = - 4
D. S = 2
Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 5 tại x = − 2 và có đồ thị đi qua điểm M (1; −1). Tính tổng S = a 2 + b 2 + c 2
A. S = −1.
B. S = 1.
C. S = 13.
D. S = 14.
Đáp án C
Từ giả thiết, ta có hệ:
− b 2 a = − 2 4 a − 2 b + c = 5 a + b + c = − 1 ⇔ a = − 2 3 ; b = − 8 3 ; c = 7 3
⇒ S = a 2 + b 2 + c 2 = 13
Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; 6). Tính tích P = abc.
A. P = -6
B. P = 6
C. P = -3
D. P = 32
a, xác định parabol y = ax^2 + bx + c đạt cực tiểu bằng 4 tại x = -2 và đồ thị đi qua A ( 0 ; 6)
b, xác định GTNN của hàm số y = x^2 - 4x + 1
a.
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-2\\4a-2b+c=4\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4a\\4a-2.4a+6=4\\c=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=4a=2\\a=\dfrac{1}{2}\\c=6\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x^2+2x+6\)
b.
\(y_{min}=y_{CT}=\dfrac{4ac-b^2}{4a}=\dfrac{4.1.1-\left(-4\right)^2}{4.1}=-3\)
Biết hs y = ax2 bx + c (a#0) đạt cực tiểu bằng 4 tại x = 2 và có đồ thị hàm số đi qua A(0;6). Tính P = abc
Thay x=0 và y=6 vào (P), ta được:
\(a\cdot0^2+b\cdot0+c=6\)
=>c=6
Vì hàm số (P) đạt cực tiểu bằng 4 khi x=2 nên ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\-\dfrac{b^2-4ac}{4a}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-b=4a\\c=6\\b^2-4ac=-16a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=6\\b=-4a\\16a^2-24a=-16a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=6\\b=-4a\\16a^2-8a=0\end{matrix}\right.\)
=>c=6; a=1/2; b=-2
=>P=-6
Xác định hàm số y = ax² + bx + c biết hàm đạt GTLN bằng 5 tại x = -2 và đồ thị hàm số đi qua điểm M(1; -1)
y = ax2 + bx + c đạt Max bằng 5 tại x = -2
--> a < 0; \(\dfrac{4ac - b^2}{4a}\) = 5;
\(\dfrac{-b}{2a}\) = -2
--> b = 4a; \(\dfrac{4ac - 16a^2}{4a}\) = 5
--> b = c - 5 = 4a
Đồ thị hàm số đi qua M(1; -1)
--> a + b + c = -1
--> a + 4a + 4a + 5 = -1
<=> 9a = -6
<=> a = \(\dfrac{-2}{3}\) --> b = \(\dfrac{-8}{3}\); c = \(\dfrac{7}{3}\)
--> \(y = \dfrac{-2}{3}x^2\ -\)\(\dfrac{8}{3}x\) + \(\dfrac{7}{3}\)
Biết rằng hàm số y= \(^{ax^2+bx+c}\) (a khác 0) đạt GTLN bằng 5 tại x = -2 và đồ thị hàm số đi qua điểm M(1;1). Tính tổng S =\(a^2+b^2+c^2\)
\(\left\{{}\begin{matrix}-\frac{b}{2a}=-2\\\frac{4ac-b^2}{4a}=5\\a+b+c=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=4a\\4ac-b^2=20a\\c=1-a-b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=4a\\4ac-b^2=20a\\c=1-5a\end{matrix}\right.\)
\(\Rightarrow4a\left(1-5a\right)-16a^2=20a\)
\(\Leftrightarrow-36a=16\Rightarrow a=-\frac{4}{9}\) \(\Rightarrow b=-\frac{16}{9};c=\frac{29}{9}\)
\(\Rightarrow S=\) bấm máy
Cho hàm số y = x3 + ax2 + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là:
A. k = 0
B. k = 24
C. k = -18
D. k = 18
Đáp án B
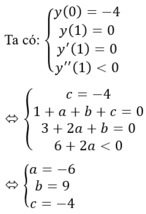
Do đó k = y’(-1) = 3 – 2a + b = 24.
Cho hàm số y = x 4 - 2 x 2 - 3 có đồ thị (C). Biết rằng parabol P : y = a x 2 + b x + c đi qua 3 điểm cực trị của đồ thị hàm số (C). Tính S=2a-2019b+c
A. S = - 2019
B. S = 5
C. S = - 5
D. S = 2019