Qua trung điểm I của đoạn thẳng BC, kẻ đường vuông góc với BC. Trên đường thẳng đó lấy điểm A
a) C/M: AI là phân giác góc BAC
b) Trên tia đói của tia IA lấy điểm D sao cho ID=IA.C/M: AB=AC=CD=DB
Qua trung điểm I của đoạn thẳng BC kẻ đường thẳng vuông góc với BC . Trên đường thẳng đó lấy điểm A .
a, CM AI là tia phân giác của góc BAC
b, Trên tia đối của tia IA lấy điểm D sao cho ID = IA . CM AB = AC = CD =DB
Cm: a) Xét t/giác ABI và t/giác ACI
có: AI : chung
\(\widehat{AIB}=\widehat{AIC}=90^0\) (gt)
BI = CI (gt)
=> t/giác ABI = t/giác ACI (c.g.c)
=> \(\widehat{BAI}=\widehat{CAI}\) (2 góc t/ứng)
=> AI là tia p/giác của góc BAC
b) Xét t/giác AIB và t/giác DIC
có: AI = DI (gt)
\(\widehat{AIB}=\widehat{CID}\) (đối đỉnh)
BI = CI (gt)
=> t/giác AIB = t/giác DIC (c.g.c)
=> AB = CD (2 cạnh t/ứng) (1)
Xét t/giác AIC và t/giác DIB
có: AI = ID (gt)
\(\widehat{AIC}=\widehat{BID}\) (đối đỉnh)
IC = IB (gt)
=> t/giác AIC = t/giác DIC (c.g.c)
=> AC = BD (2 cạnh t/ứng) (2)
Mà AB = AC (vì t/giác AIB = t/giác AIC) (3)
Từ (1); (2) và (3) => AB = AC = CD = DB
qua trung điểm I của đoạn thẳng BC , kẻ đg' thg vuông góc vs BC . trên đg' thg đó lấy điểm A
a. c/m AI là tia p/g góc BAC
b. trên tia đối của tia IA lấy điểm d sao cho ID = IA , c/m AB = AC = CD = DB
qua trung điểm I của đoạn thẳng BC. Kẻ đường thẳng vuông góc với BC. Trên đường thẳng đó lấy điểm E.
a) Chứng minh Ay là tia phân giác của góc BAC.
b) Trên tia đối của tia yA lấy điểm D sao cho yD=yA. Chứng minh AB=AC=CD=DB.
a: Xét ΔABC có
AI là đường trung tuyến
AI là đường cao
Do đó: ΔABC cân tại A
hay AI là tia phân giác của góc BAC
b: Xét tứ giác ABDC có
I là trung điểm của AD
I là trung điểm của BC
Do đó: ABDC là hình bình hành
mà AB=AC
nên ABDC là hình thoi
=>AB=AC=CD=DB
a: Xét ΔABC có
AI là đường trung tuyến
AI là đường cao
Do đó: ΔABC cân tại A
hay AI là tia phân giác của góc BAC
b: Xét tứ giác ABDC có
I là trung điểm của AD
I là trung điểm của BC
Do đó: ABDC là hình bình hành
mà AB=AC
nên ABDC là hình thoi
AB=AC=CD=DB
Qua trung điểm I của đoạn thẳng BC, kẻ đường vuông góc với BC. Trên đường thẳng đó lấy điểm A.
a) CMR: AI là tia phân giác của BAC
b) Trên tia đối của tia IA lấy điểm D sao cho ID=IA.
Chứng minh: AB= AC= CD= DB.
Các bạn giúp mik bài này với nhé![]()
a)
Xét \(\Delta AIB\) và \(\Delta AIC\) có :
IB = IC ( gt )
Chung AI
\(\widehat{I_1}=\widehat{I_2}=90^0\)
=> \(\Delta AIB\) = \(\Delta AIC\)
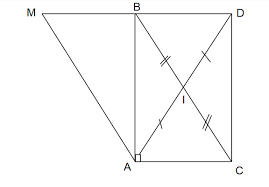
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)=> AI là tia phân giác của góc BAC=> AB = ACb)C/m tương tự ta => BC = BD ; AB = AD=> AB = BC = CD = DACho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID = IA CMR: CMR: Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. Chứng minh CMR: AB là tia phân giác của góc DAM
a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đối đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM
Cho tam giác ABC có AB = AC, I là trung điểm của BC.
a) Chứng minh AI vuông góc với BC
b) Trên tia đối của tia IA lấy điểm D sao cho IA = ID, chứng minh AB = CD
c) Trên một nửa mặt phẳng bờ là đường thẳng BC, không chứa điểm A, kẻ BE vuông góc với BC, BE = AI. O là trung điểm của BI, chứng minh A, O, E thẳng hàng.
d) Biết góc BEI bằng 400 tính số đo góc ACB.
Cho tam giác ABC có AB = AC, góc A là góc nhọn, H là trung điểm của BC.
a) Chứng minh AH là tia phân giác của góc BAC
b) Vẽ HD vuông góc với AC tại D. Trên cạnh AB lấy điểm E sao cho AE = AD. Tính số đo góc AEH.
Gọi M là giao điểm của hai tia AB và DH. Đường thẳng qua M và song song với ED cắt tia AC tại N. Chứng minh N, H, E thẳng hàng.
Cho tam giác ABC có AB = AC, góc A là góc nhọn, H là trung điểm của BC.
a) Chứng minh AH là tia phân giác của góc BAC
b) Vẽ HD vuông góc với AC tại D. Trên cạnh AB lấy điểm E sao cho AE = AD. Tính số đo góc AEH.
Gọi M là giao điểm của hai tia AB và DH. Đường thẳng qua M và song song với ED cắt tia AC tại N. Chứng minh N, H, E thẳng hàng.
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AM=IK b) Tam giác AMI bằng tam giác IKC c) AI=IC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân giác cuả góc DAM Bài 3: Cho tam giác ABC vuông ở A và AB=AC.Gọi K là trung điểm của BC a) C/M: tam giác AKB bằng tam giác AKC b) C/M: AK vuông góc với BC c) từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E.C/M EK song song với AK Bài 4: Cho tam giác ABC có AB=AC, kẻ BD vuông góc với AC, CE vuông góc với AB(D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CMR a) BD= CE b) tam giác OEB bằng tam giác ODC c) AO là tia phân giác cua góc BAC
1. Câu hỏi của 1234567890 - Toán lớp 7 - Học toán với OnlineMath
Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA
a) CMR tam giác BID bằng tam giác CIA
b) CMR : BD vuông góc với AB
c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC
d) CMR: AB là tia phân giác cuả góc DAM
Em tham khảo nhé!
Câu hỏi của Vy Hà Khánh - Toán lớp 7 - Học toán với OnlineMath