chứng minh rằng với mọi số tự nhiên n thì các cặp số nguyên tố sau cùng nhau;
a.(2n+2)và(2n+1)
b.(2n+1)và(4n+3)
c.(9n+4)và(12n+5)
giúp mk nhanh lên nhé,chiều mai mk nộp bài rồi các bạn ơi,mà giải cụ thể cho mk nhé,cảm ơn các bạn
a) chứng minh rằng khi nla số tự nhiên khác 0 thì n+1 là 2 số nguyên tố cùng nhau.
b)chứng minh rằng với mọi số tự nhiên n thì các số sau là nguyên tố cùng nhau :2n+3 va 4n+8
e có 2 chia hết cho d; 2n+3 lẻ nên (2n+3,4n+8)=1
còn n+1-n=1 nên (n,n+1)=1
Chứng minh rằng cặp số sau nguyên tố cùng nhau với mọi số tự nhiên n:
n và n+1
Gọi d là ƯCLN của n và n+1
=> n chia hết cho d;n+1 chia hết cho d
=> n+1-n chia hết cho d
=> 1 chia hết cho d
=> d = 1
Vậy n và n+1 nguyên tố cùng nhau với mọi n
Với mọi số tự nhiên n, chứng minh rằng các cặp số sau nguyên tố cùng nhau:
a) 2n + 3, n + 2
b) n + 1, 3n +4
c) 2n + 3, 3n + 4
Gọi d là ước chung lớn nhất của 2 số. Nhiệm vụ của ta là chứng minh d=1.
a) 2n+3, n+2 \(⋮d\)
\(\Rightarrow\left(2n+3\right)-\left(n+2\right)⋮d\)
\(\Rightarrow1⋮d\)
b) n+1, 3n+4
\(\Rightarrow\left(3n+4\right)-3\left(n+1\right)⋮d\)
\(\Rightarrow1⋮d\)
c) 2n+3, 3n+4
\(\Rightarrow3\left(2n+3\right)-2\left(3n+4\right)⋮d\)
\(\Rightarrow1⋮d\)
𝓪, 𝓖𝓸̣𝓲 𝓤̛𝓒𝓛𝓝\(\left(2n+3,n+2\right)=d\)
\(\Rightarrow2n+3⋮d\)
\(\Rightarrow n+2⋮d\Rightarrow2.\left(n+2\right)⋮d\Rightarrow2n+4⋮d\)
\(\Rightarrow2n+4-2n+3⋮d\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow\)𝓤̛𝓒𝓛𝓝\(\left(2n+3,n +2\right)=1\)
𝓥𝓪̣̂𝔂 \(2n+3,n+2\) 𝓵𝓪̀ 𝓱𝓪𝓲 𝓼𝓸̂́ 𝓷𝓰𝓾𝔂𝓮̂𝓷 𝓽𝓸̂́ 𝓬𝓾̀𝓷𝓰 𝓷𝓱𝓪𝓾
𝓫, 𝓖𝓸̣𝓲 𝓤̛𝓒𝓛𝓝\(\left(n+1,3n+4\right)=d\)
\(\Rightarrow3n+4⋮d\)
\(\Rightarrow n+1⋮d\Rightarrow3\left(n+1\right)⋮d\Rightarrow3n+3⋮d\)
\(\Rightarrow3n+4-\left(3n+3\right)⋮d\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow\)𝓤̛𝓒𝓛𝓝\(\left(n+1,3n+4\right)=1\)
𝓥𝓪̣̂𝔂 \(n+1,3n+4\) 𝓵𝓪̀ 𝓱𝓪𝓲 𝓼𝓸̂́ 𝓷𝓰𝓾𝔂𝓮̂𝓷 𝓽𝓸̂́ 𝓬𝓾̀𝓷𝓰 𝓷𝓱𝓪𝓾
𝓑𝓪̣𝓷 𝓸̛𝓲, 𝓬𝓱𝓸 𝓶𝓲̀𝓷𝓱 𝓼𝓾̛̉𝓪 𝓵𝓪̣𝓲 𝓸̛̉ 𝓬𝓪̂𝓾 𝓪 𝓷𝓱𝓪, 𝓬𝓱𝓸̂̃ 2𝓷+4-(2𝓷+3) 𝓹𝓱𝓪̉𝓲 𝓽𝓱𝓮̂𝓶 𝓷𝓰𝓸𝓪̣̆𝓬 𝓸̛̉ 2𝓷+3 𝓷𝓱𝓪!
1.Chứng minh rằng: Với mọi số tự nhiên các số sau là các số nguyên tố cùng nhau.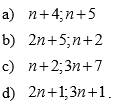
2.Tìm các số tự nhiên để các số sau nguyên tố cùng nhau. 
1:
a: Gọi d=ƯCLN(n+5;n+4)
=>\(\left\{{}\begin{matrix}n+5⋮d\\n+4⋮d\end{matrix}\right.\)
=>\(n+5-n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>n+4 và n+5 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(2n+5;n+2)
=>\(\left\{{}\begin{matrix}2n+5⋮d\\n+2⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+4⋮d\end{matrix}\right.\)
=>\(2n+5-2n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+5 và n+2 là hai số nguyên tố cùng nhau
c: Gọi d=ƯCLN(3n+7;n+2)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\3n+6⋮d\end{matrix}\right.\)
=>\(3n+7-3n-6⋮d\)
=>\(1⋮d\)
=>d=1
=>3n+7 và n+2 là hai số nguyên tố cùng nhau
d: Gọi d=ƯCLN(2n+1;3n+1)
=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+1⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+2⋮d\end{matrix}\right.\)
=>\(6n+3-6n-2⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+1 và 3n+1 là hai số nguyên tố cùng nhau
a) Gọi d là ƯCLN của n + 4 và n + 5
⇒ n + 4 ⋮ d và n + 5 ⋮ d
⇒ (n + 5 - n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 4 và n + 5 luôn là cặp SNT cùng nhau
b) Gọi d là ƯCLN của 2n + 5 và n + 2
⇒ 2n + 5 ⋮ d và n + 2 ⋮ d
⇒ 2n + 5 ⋮ d và 2(n + 2) ⋮ d
⇒ (2n + 5 - 2n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 5 và n + 2 luôn là cặp SNT cùng nhau
c) Gọi d là ƯCLN của n + 2 và 3n + 7
⇒ n + 2 ⋮ d và 3n + 7 ⋮ d
⇒ 3(n + 2) ⋮ d và 3n + 7 ⋮ d
⇒ (3n + 7 - 3n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 2 và 3n + 7 luôn là cặp SNT cùng nhau
d) Gọi d là ƯCLN của 2n + 1 và 3n + 1
⇒ 2n + 1 ⋮ d và 3n + 1 ⋮ d
⇒ 3(2n + 1) ⋮ d và 2(3n + 1) ⋮ d
⇒ (6n + 3 - 6n - 2) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 1 và 3n + 1 luôn là cặp SNT cùng nhau
chứng minh rằng với mọi số tự nhiên n,các số sau là các số nguyên tố cùng nhau
a) n+1;n+2
b) 3n+10;3n+9
(Nếu ƯCLN(a,b)= thì hai số a,b được gọi là hai số nguyên tố cùng nhau)
*giúp tui vớiiiiiiiiiii*
\(a,\) Gọi \(d=ƯCLN\left(n+1;n+2\right)\)
\(\Rightarrow n+1⋮d;n+2⋮d\\ \Rightarrow n+2-n-1⋮d\\ \Rightarrow1⋮d\\ \Rightarrow d=1\)
Vậy \(ƯCLN\left(n+1;n+2\right)=1\) hay n+1 và n+2 ntcn
\(b,\) Gọi \(d=ƯCLN\left(3n+10;3n+9\right)\)
\(\Rightarrow3n+10⋮d;3n+9⋮d\\ \Rightarrow3n+10-3n-9⋮d\\ \Rightarrow1⋮d\\ \Rightarrow d=1\)
Vậy 3n+10 và 3n+9 ntcn
Chứng minh rằng: với mọi số tự nhiên thì n+1vaf 3n+4 là các số nguyên tố cùng nhau
1 chứng minh rằng với mọi số tự nhiên n, các số sau nguyên tố cùng nhau
n+1 và 2n+1
b: Gọi d=ƯCLN(2n+1;n+1)
=>2n+1 chia hết cho d và n+1 chia hết cho d
=>2n+2 chia hết cho d và 2n+1 chia hết cho d
=>2n+2-2n-1 chia hết cho d
=>1 chia hết cho d
=>d=1
=>ĐPCM
chứng minh rằng các cặp số tự nhiên sau nguyên tố cùng nhau với mọi n thuộc N
n và 2n+1
L:
a) Gọi d là UCLN ( n ; n+1 )
n+1 chia hết cho d
n chia hết cho d
-> n+1-n chia hết cho d
-> 1chia hết cho d
=>N và n+1 là 2 số nguyên tố cùng nhau
=>ĐPCM
^HT^
Chứng tỏ rằng các cặp số sau nguyên tố cùng nhau với mọi số tự nhiên n: a, 2n + 1 và 6n + 5 b, 3n + 2 và 5n + 3
a: Gọi d=ƯCLN(6n+5;2n+1)
=>\(\left\{{}\begin{matrix}6n+5⋮d\\2n+1⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+5⋮d\\6n+3⋮d\end{matrix}\right.\Leftrightarrow6n+5-6n-3⋮d\)
=>\(2⋮d\)
mà 2n+1 là số lẻ
nên d=1
=>2n+1 và 6n+5 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(3n+2;5n+3)
=>\(\left\{{}\begin{matrix}3n+2⋮d\\5n+3⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}15n+10⋮d\\15n+9⋮d\end{matrix}\right.\)
=>\(15n+10-15n-9⋮d\)
=>\(1⋮d\)
=>d=1
=>3n+2 và 5n+3 là hai số nguyên tố cùng nhau
1.Chứng tỏ rằng hai số lẻ liên tiếp là hai số nguyên tố cùng nhau
2.Chứng minh rằng với mọi số tự nhiên , các số sau là các số nguyên tố cùng nhau.
a) n+1 và n+2 b)2n+2 và 2n+3
c)2n+1 và n+1 d)n+1 và 3n+4
Bài 1: Gọi hai số lẻ liên tiếp là $2k+1$ và $2k+3$ với $k$ tự nhiên.
Gọi $d=ƯCLN(2k+1, 2k+3)$
$\Rightarrow 2k+1\vdots d; 2k+3\vdots d$
$\Rightarrow (2k+3)-(2k+1)\vdots d$
$\Rightarrow 2\vdots d\Rightarrow d=1$ hoặc $d=2$
Nếu $d=2$ thì $2k+1\vdots 2$ (vô lý vì $2k+1$ là số lẻ)
$\Rightarrow d=1$
Vậy $2k+1,2k+3$ nguyên tố cùng nhau.
Ta có đpcm.
Bài 2:
a. Gọi $d=ƯCLN(n+1, n+2)$
$\Rightarrow n+1\vdots d; n+2\vdots d$
$\Rightarrow (n+2)-(n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $(n+1, n+2)=1$ nên 2 số này nguyên tố cùng nhau.
b.
Gọi $d=ƯCLN(2n+2, 2n+3)$
$\Rightarrow 2n+2\vdots d; 2n+3\vdots d$
$\Rightarrow (2n+3)-(2n+2)\vdots d$ hay $1\vdots d$
$\Rightarrow d=1$.
Vậy $(2n+2, 2n+3)=1$ nên 2 số này nguyên tố cùng nhau.
Bài 2:
c.
Gọi $d=ƯCLN(2n+1, n+1)$
$\Rightarrow 2n+1\vdots d; n+1\vdots d$
$\Rightarrow 2(n+1)-(2n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $ƯCLN(2n+1, n+1)=1$ nên 2 số này nguyên tố cùng nhau.
d.
Gọi $d=ƯCLN(n+1, 3n+4)$
$\Rightarrow n+1\vdots d; 3n+4\vdots d$
$\Rightarrow 3n+4-3(n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $ƯCLN(n+1, 3n+4)=1$
$\Rightarrow$ 2 số này nguyên tố cùng nhau.