`@` `\text {Ans}`

`\downarrow`

`a,`

Vì `\Delta ABC` cân tại A

`-> \text {AB = AC,}` $\widehat {B} = \widehat {C}$

Vì `\text {AH}` là đường cao

`-> \text {AH} \bot \text {BC}`

`->` $\widehat {AHB} = \widehat {AHC} = 90^0$

Xét `2 \Delta` vuông `AHB` và `AHC`:

`\text {AB = AC}`

$\widehat {B} = \widehat {C}$

`=> \Delta AHB = \Delta AHC (ch-gn)`

`b,`

Vì `\Delta AHB = \Delta AHC (a)`

`-> \text {HB = HC (2 cạnh tương ứng)}`

`-> \text {H là trung điểm của BC}` 

Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)

Vì `\Delta ABC` cân tại A.

Mà `\text {AH}` là đường cao

`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`

`-> \text {AH cũng là đường trung tuyến}`

`-> \text {H là trung điểm của BC}`

`c,`

Vì `\Delta AHB = \Delta AHC (a)`

`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$

`-> \text {AH là tia phân giác của} \Delta ABC`

Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)

Vì `\Delta ABC` cân tại A.

Mà `\text {AH}` là đường cao

`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`

`-> \text {AH cũng là đường phân giác}`

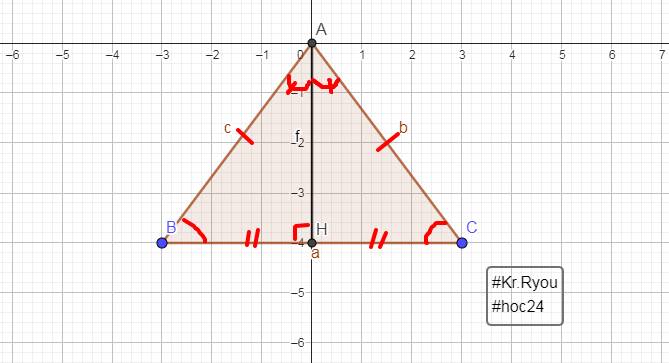
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

=>ΔAHB=ΔAHC

b: ΔAHB=ΔAHC

=>HB=HC

=>H là trung điểm của BC

c: ΔABC cân tại A

mà AH là trung tuyến

nên AH là phân giác 

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

góc B chung

=>ΔHBA đồng dạng với ΔABC

b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

AH=3*4/5=2,4cm

a. Xét ΔHBA và ΔABC có:

       \(\widehat{H}=\widehat{A}\) = 90⁰ (gt)

        \(\widehat{B}\) chung

\(\Rightarrow\)  ΔHBA \(\sim\) ΔABC (g.g)

b. Vì  ΔABC vuông tại A

Theo đ/lí Py - ta - go ta có:

  BC² = AB² + AC²

  BC² = 3² + 4²

\(\Rightarrow\) BC² = 25 cm

\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm

Ta lại có:  ΔHBA \(\sim\) ΔABC

   \(\dfrac{AH}{CA}=\dfrac{BA}{BC}\) 

\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\) 

\(\Rightarrow\) AH = 2,4 cm

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)

nên ΔABC vuông tại A

b: Xét ΔAHC vuông tại H có \(\widehat{C}=45^0\)

nên ΔAHC vuông cân tại H

=>\(AH=HC=\dfrac{BC}{2}=\dfrac{5}{2}\sqrt{2}\left(cm\right)\)

a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A

\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)

\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)

* Áp dụng hệ thức : 

\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)

\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)

\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm 

\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm

\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)

Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm²

b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)

Lại có : \(BC=BD+DC=15+20=35\)cm 

Áp dụng định lí Pytago cho tam giác ABC vuông tại A

\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)

\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm 

\(\Rightarrow AB=\frac{3}{4}.28=21\)cm 

* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)

\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm 

* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm 

\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm

Áp dụng định lí Pytago cho tam giác AHD vuông tại H 

\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm 

tam giác AHB vuông tại H ,THEO ĐỊNH LÝ PYTA GO TA CÓ

AB^2=AH^2+BH^2=>AB^2=169=>AB=13 CM

TAM GIÁC AHC VUÔNG TẠI H,THEO ĐỊNH LÝ PYTA GO TA CÓ

HC^2+AH^2=AC^2=>HC^2=AC^2-AH^2=>HC^2=256=>HC=16CM

VÌ H NẰM GIỮA BC => BC=BH+HC=21 CM

=>CHU VI TAM GIÁC ABC LÀ

AB+AC+BC=13+21+20=54 CM

\(\dfrac{AI}{AH}=\dfrac{4}{5}\)

=>\(AI=\dfrac{4}{5}AH\)

Ta có: AI+HI=AH

=>\(HI=AH-AI=AH-\dfrac{4}{5}AH=\dfrac{1}{5}AH\)

\(\dfrac{AI}{IH}=\dfrac{\dfrac{4}{5}AH}{\dfrac{1}{5}AH}=\dfrac{4}{5}:\dfrac{1}{5}=4\)

Xét ΔBAH có BI là phân giác

nên \(\dfrac{BA}{BH}=\dfrac{AI}{IH}\)

=>\(\dfrac{10}{BH}=4\)

=>BH=10/4=2,5(cm)

ΔABC cân tại A có AH là đường cao

nên H là trung điểm của BC

=>\(BC=2\cdot BH=5\left(cm\right)\)

Chu vi tam giác ABC là:

10+10+5=25(cm)

Hình vẽ:

Giải

a. Xét ΔHBA và ΔABC có:

\(\widehat{B}\)  chung

\(\widehat{BHA}=\widehat{BAC}=90^0\)

⇒ΔHBA ∼ ΔABC (g.g)

b. Xét ΔABC vuông tại A có:

\(BC^2=AB^2+AC^2\)(định lí py-ta-go)

         \(=5^2+12^2\)

         \(=169\)

\(\rightarrow BC=\sqrt{169}=13\left(cm\right)\)

Vì ΔABC ∼ ΔHBA (cmt)

\(\rightarrow\dfrac{AB}{BH}=\dfrac{AC}{AH}=\dfrac{BC}{AB}hay\dfrac{5}{BH}=\dfrac{12}{AH}=\dfrac{13}{5}\)

⇒\(BH=\dfrac{5.5}{13}=\dfrac{25}{13}\left(cm\right)\)

⇒\(AH=\dfrac{12.5}{13}=\dfrac{60}{13}\left(cm\right)\)